A more powerful technique than TD-PSOLA, linear prediction can manipulate source and filter separately.

Join smoothing
To understand the power of linear predictive waveform coding, we'll consider the problem of smoothing the joins in concatenative synthesis.

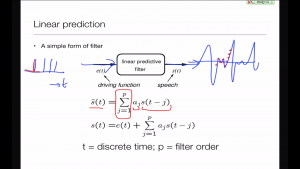
The filter
It's just a simple equation, but for this course we don't need to get too deep into the maths.

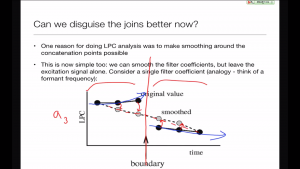
Performing join smoothing
Now we understand how linear predictive coding works, we can use it to smooth the spectral envelope across joins.

Filter parameter update
Since the filter is time-varying, we need to decide how frequently (and at what moments in time) to update its co-efficients.

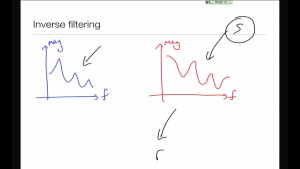
Inverse filtering
Exciting the filter with a simple pulse train doesn't produce good quality. Fortunately, there is an almost-perfect excitation signal: the residual.