Weighting diagonal steps differently

[Eoin M]

In the slides you state that the ‘Number of local distances summed is path dependent, since paths vary in their length’, and that the solution to this is to ‘weight diagonal steps differently to horizontal or vertical ones’.

Could you explain this point in more detail since I don’t quite see how one thing follows from the other?

Thank you!

[Simon]

Think about the grid, which is the data structure used for Dynamic Time Warping. Paths from one corner to the diagonally-opposite corner must pass through the points on the grid, summing up local distances as they go. Paths close to the main diagonal generally pass through fewer points in total than paths that stray far away from the main diagonal.

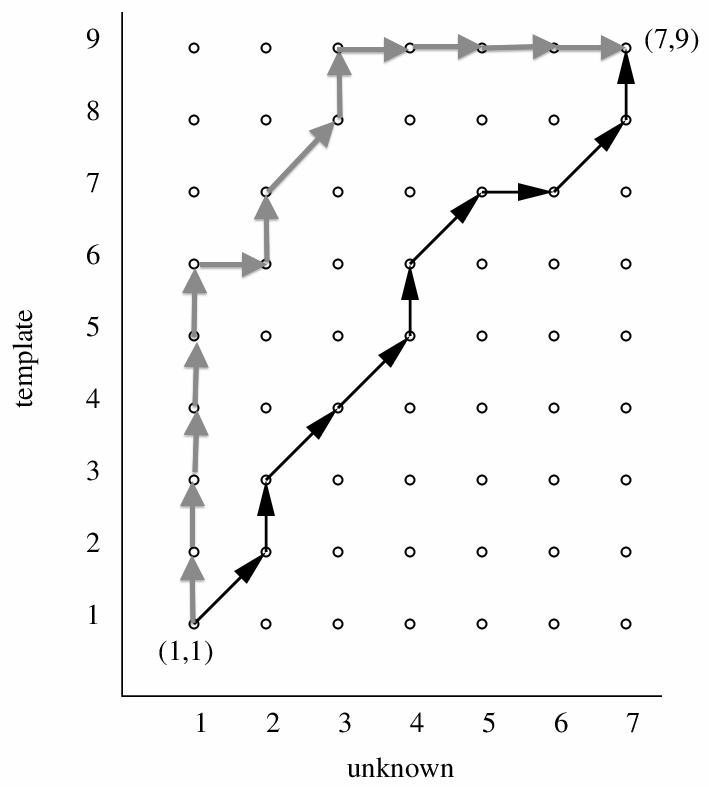
You can see in the diagram above how the two paths differ in the number of local distances that they must sum up. This leads to a bias in favour of paths that stay close the the main diagonal.

To reduce this bias, lots of solutions were proposed back at the time when DTW was the state-of-the-art. One is to penalise diagonal paths (e.g., add a penalty cost to the distance-so-far every time a diagonal move is made). One popular method was to impose local constraints, such as in this diagram (the numbers are weights or penalty terms):

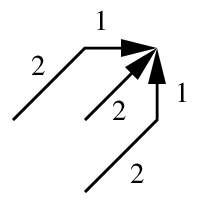
Is this still important?

For automatic speech recognition, this is all outdated and no longer important. But there is a general lesson that might apply to other applications of dynamic programming: look for biases towards certain solutions, and ask whether that needs to be compensated for.

[Author]

Posts