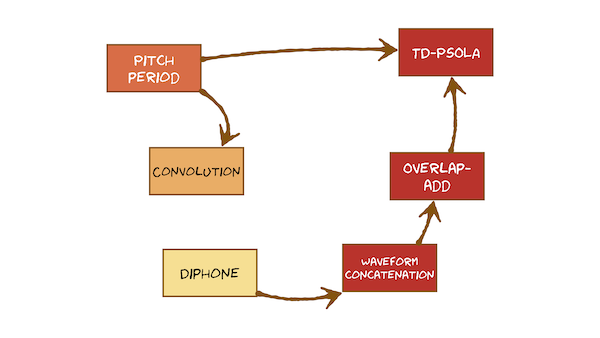
It’s time to bring together everything we learned earlier about speech signals and the source-filter model, and use that to develop a method for creating synthetic speech. This course only covers one method, which uses a database of recorded natural speech from which small waveform fragments are selected and then concatenated. These waveform fragments are of special sub-word units called diphones. Because they are taken from natural recordings, they will have an F0 and duration but these might not match the values we predicted in the front end. Therefore a method is needed to modify these properties, without changing the spectral envelope.
Here’s what you’re going to learn in the videos:
Lecture Slides
Slides for Thursday lecture (google) [updated 22/10/2024]
Total video to watch in this section: 38 minutes
This video just has a plain transcript, not time-aligned to the videoIt's finally time to think about how to make synthetic speech.The obvious approach is to record all possible speech sounds, and then rearrange them to say whatever we need to say.So then the question is, what does 'all possible speech sounds' actually mean?To make that practical, we'd need a fixed number of types so that we can record all of them and store them.I hope it's obvious that words are not a suitable unit, because new words are invented all the time.We can't record them all, for the same reason we could never write a dictionary that has all of the words of the language in it.We need a smaller unit than the word: a sub-word unit.So how about recordings of phonemes?Well, a phoneme is an abstract category, so when we say it out loud and record it, we call it a 'phone'.As we're about to see, phones are not suitable, but we can use them to define a suitable unit called the diphone.Consider how speech is produced.There is an articulatory target for each phone that we need to produce, to generate the correct acoustics, and that's so the listener hears the intended phone.Speech production has evolved to be efficient, and that means minimising the energy expended by the speaker and maximising the rate of information.That means that this target is only very briefly achieved before the talker very quickly moves on towards the next one.I'm going to illustrate that using the second formant as an example of an acoustic parameter that is important for the speaker to produce, so that the listener hears the correct phone.These are just sketches of formant trajectories, so I'm not going to label the axes too carefully.This is, of course, 'time'.The vertical axis is formant frequency.To produce this vowel, the speaker has to reach a particular target value of F2.It's the same in both of these words, because it's the same vowel.That target is reached sufficiently accurately and consistently for the listener to be able to hear that vowel.But look at the trajectory of that formant coming in to the target and leaving the target.Near the boundaries of this phone, there's a lot of variation in the acoustic property.Most of that variation is the consequence of the articulators having to arrive from the previous target or start moving towards the next target.In other words: the context in which this phone is being produced.For example, here the tongue was configured to produce [k] and then had to move to the position for the vowel [æ] and it was still on the way towards that target when voicing had commenced.In other words, the start of the vowel is strongly influenced by where the tongue was coming from.The same thing happens at the end.The tongue is already heading off to make the next target for the [t] before the vowel is finished.So the end of the vowel is strongly influenced by the right context.Imagine we wanted to re-use parts of these recordings to make new words that we hadn't yet recorded.Could we just segment them into phones and use those as the building blocks?Let's try that.Clearly, the [æ] in [k æ t] and the [æ] in [b æ t] are very different because of this contextual variation near the boundaries of the phone.That means that we can't use an [æ] in [k æ t] to say [b æ t]: these are not interchangeable.We're looking for sounds to be interchangeable so we can rearrange them to make new words.There's a very simple way to capture that context-dependency, and that's just to redefine the unit from the phone to the diphone.Diphones have about the same duration as a phone, but their boundaries are in the centres of phones.They are the units of co-articulation.Now look what happens.The æ-t diphone in [k æ t] is very similar to the one in [b æ t], and these two sound units are relatively interchangeable.We could use the æ-t diphone from [k æ t] to say [b æ t] or any other word involving æ-t.W've simply redefined units from phones to diphones.Diphones are units of co-articulation.Now, of course, co-articulation spreads beyond just the previous or next phone.This is just a first-order approximation, but it's much better than using context-independent phones as the building blocks for generating speech.These two phones sound very different, because of context: they're not interchangeable.They're not useful for making any new word with an [æ] in it.In contrast, these two diphones sound very similar: they are relatively interchangeable.We can use them to make new words requiring the [æ t] sequence.They capture co-articulation.Obviously, there's going to be rather more types of diphone than there are of phone.If we have 45 phone classes, we're going to need 46^2 classes of diphone, roughly.Not all are possible, but most are.Why 46?Because diphones need to have silence: the IPA forgot about that.There are a lot more diphone types than phone types, but it's still a closed set, and it's very manageable.If we record an inventory of natural spoken utterances and segment them into diphones, we can extract those diphones and rearrange them to make new utterances.Here's a toy example, using just a few short phrases.In general, we would actually have a database of 1000s or 10 000s of recorded sentences.This picture is the database.These are natural sentences, segmented into diphones.Now let's make an utterance that was not recorded.In other words, let's do speech synthesis!This word is not in the database.We've created it - we've synthesised it - by taking diphones (or short sequences of diphones) from the database and joining them together.There's actually more than one way to make this word from that database.Here's another way.This way involves taking longer contiguous sequences of diphones and only making a join here; that might sound better.The phone is not a useful building block directly, but we can use to define the diphone, which is a useful building block for synthesising speech.We make new utterances by rearranging units from recorded speech.The smallest unit we'll ever take is the diphone, but we already saw in the toy example that taking sequences of diphones is also possible.That will involve making fewer joins between the sequences and it'll probably sound better, on average.The key point here is that the joins in the synthetic speech will always be in the middle of phones and never at phone boundaries.I've said that we're going to join sequences of diphones together, so the next step is actually to define precisely how that's done.We need a method for concatenating recorded waveforms.
This video just has a plain transcript, not time-aligned to the videoWe've defined the diphone and decided that it's a suitable unit for building new spoken utterances.That's because it captures co-articulation, at least locally.If we had a recorded database of speech containing at least one example of every possible diphone, we could simply concatenate diphone units (or sequences of diphone units) taken from those recordings, to create any new utterance we like.Now we going to make a first attempt at waveform concatenation to discover whether it really is that simple.Here are two diphone sequences.On the left k-æ and on the right æ-t.I'm going to use them to make a synthetic version of the word 'cat'.So I'll simply concatenate them: join them together, like that.It sounds like this: 'cat'Let's hear that again: 'cat'There's a distinct click in the middle.Let's see why that is.Zoom in, and we can see at the concatenation point (often simply, we say 'the join'), we can see a big discontinuity there.We need to be a little bit more careful about where and how we make the join.One option would obviously be to join the waveforms only at a point where they have the same amplitude, so we don't get the discontinuity.One such point is where they both cross zero: at a zero crossing.Here's a new version then, where the waveforms are joined at a zero crossing.That's the zero crossing.We've got no sudden discontinuity.It sounds like this: 'cat'.The click has gone, which is good, but the join is still audible.One reason the join might be audible is the following problem.I've zoomed back out a little bit, so we can clearly see the fundamental periods of the signal.Those are coming from the sound source, which of course here is the vocal folds, because this is voiced speech.The periodicity here does not properly align as we transition from one diphone to the next.The periods aren't evenly spaced.So we can do even better than this, even better than joining it at zero crossings.We can join in a way that is called 'pitch-synchronous'.That's going to involve adjusting the end point of the first diphone or the start point of the second diphone to keep the periodicity intact across the join.To make pitch-synchronous joins, we need to annotate the waveform with a single consistent moment in time within each fundamental period that corresponds to the activity of the vocal folds.Since we don't have access to the vocal folds of the speaker, we can only estimate these moments in time from the waveform.That process is known as 'pitch marking'.We're not going to describe the algorithm for doing pitch marking here.Just assume that there is one and it's possible.We'll have an algorithm that will find the fundamental periods and place a mark at a consistent point in each of them.We should give a slightly more careful definition of some terms.The term 'epoch' is used to indicate the moment of closure of the vocal folds.That's a physical event during speech production, and we don't have direct access to that from the waveform.A 'pitch mark'- which these are - is our estimate of the epoch, annotated onto a speech waveform.In the literature, you'll find the terms 'epoch' and 'pitch mark' sometimes used interchangeably, even though they're not quite the same thing.Here's our final way of concatenating the two waveforms, this time making sure the join is placed in a way that preserves the fundamental periodicity.That is, so that the pitch marks are correctly spaced around the join.If we zoom in, we can now see that the fundamental period is consistent across the join.We can barely see where the join is.It sounds like this: 'cat'.The only evidence remaining of the join really is this change in amplitude.We can still hear it a little.We could still do better than that.But this is our best way yet of concatenating two waveforms.Let's compare the three methods.The very naive way: 'cat'.There was a big click because we didn't take care as to where we joined the waveforms.Joining at a zero crossing: 'cat' - a less perceptible join.Joining pitch-synchronously: 'cat'.You might not hear much difference between the last two in this example, but pitch-synchronous joins are, on average, slightly less perceptible than zero-crossing joins.That will matter much more when we're constructing a longer utterance with many waveform concatenation points.We've learned, then, that care is needed when concatenating waveforms in order to minimise the chance that the listener will hear the join.We can still do better.You'll have noticed that the two diphone sequences I joined here had noticeably different amplitudes, and that was audible.The fundamental frequency might also suddenly change at a concatenation point, and that will be audible too.We need to develop a slightly more powerful way to manipulate speech that can solve these problems, to minimise the chance that a join is audible.
This video just has a plain transcript, not time-aligned to the videoWe're synthesising speech by joining together recorded diphones: by concatenating their waveforms.We've seen waveform concatenation must be done with care.That's actually something that's true in general about signal processing.Signal processing isn't just about theory; it's about the details and the care of the implementation.We found that joining at zero crossings was much better than joining at an arbitrary point, but that a pitch-synchronous concatenation point can further reduce the chances of a join being audible.But in general, it might not be possible to always find a place where the pitch marks are nicely spaced and there's a zero crossing.So we need a more general-purpose method to make smooth sounding joins in all possible cases.That actually turns out to be rather simple: by cross-fading.That's called overlap-add.Here's the solution.As one song comes the end, this DJ has the next song ready on the other deck.The DJ makes sure the two songs have a similar tempo and that the beats are aligned, then fades out the previous song whilst fading in the next song.If the DJ does a good job of that, no one on the dance floor will notice and everyone keeps dancing happily.We've already got our beats aligned by making pitch-synchronous joins.Now we'll add the fade-out of the previous waveform while fading in the next one.Here are two waveforms I'd like to concatenate.I'm just going to simply fade out the first one.In other words, I'm going to reduce the volume just at the end, down to zero, smoothly.I'm going to fade in the second one: increase the volume from zero, smoothly.Then overlap and add them.Apply that fade out and fade in: that just scales down the amplitude to zero, smoothly.I overlap them, and where the samples overlap, I'll sum them, I'll add them together.Hence the name of the method: 'overlap-add'.Here are the waveforms concatenated using overlap-add.Now the join is quite hard to spot.Overlap-add is a very general method; it's very useful.But we're not quite as good as the DJ yet.We've not taken care to match the fundamental period of the two waveforms before joining them.So there may still be an audible discontinuity in the pitch.Sudden changes in pitch are not natural and listeners will notice them.You'll also remember that our front end has predicted values for F0 and for duration.So we need a method to impose those onto the recorded speech because, in general, our recorded diphones won't have the desired F0 or duration that our front end predicted.There's a single solution to all of those problems: a method for modifying both the fundamental frequency and the duration of speech directly on waveforms, called Time-Domain Pitch-Synchronous Overlap-and-Add.Before understanding that, we'll need to revisit the concept of the pitch period, which will be the fundamental unit on which Time-Domain Pitch-Synchronous Overlap-and-Add will work, and remind ourselves how the pitch period relates the source-filter model.Once we've done that, we can combine the idea of the pitch period with the technique of overlap-add and understand this powerful algorithm Time-Domain Pitch-Synchronous Overlap-and-Add, or TD-PSOLA for short.
This video just has a plain transcript, not time-aligned to the videoWe're going to talk a bit more about the concept of the pitch period.We're going to remind ourselves how that relates to the source-filter model.We take an impulse train and we pass it through a filter with resonances.We can generate speech with the source-filter model.One way to understand the filter is through its impulse response.That is, we put a single impulse into the filter and observe the waveform that we get out.That waveform is a pitch period.Using this idea, we'll devise a way to break a natural speech signal down into a sequence of pitch periods, which later we can use to manipulate that speech signal.Here's a short fragment of voiced natural speech.The source-filter model tells us that this was generated using a simple excitation signal from the vocal folds (idealised as an impulse train in the model) passed through the vocal tract filter.So this signal is a sequence of vocal tract impulse responses.We need to separate the source and the filter so that we can manipulate them separately.For example, to modify the fundamental frequency (F0) without changing the identity of the phone, we just need to manipulate the source and leave the filter alone.We need to identify the filter from this signal so that we can preserve it.One way to do that, of course, would be to fit a source-filter model and solve for the filter coefficients.But remember that there are several ways to represent the filter, all containing the same information but in different domains.Those coefficients (of the difference equation) are just one representation.We could also talk about the frequency response of the filter, or about its impulse response.The impulse response exists in the time domain.So there is a way to get hold of the filter right here in the time domain.We're going to use the impulse responses as our representation of the vocal tract filter.That will require us to find the fundamental periods of the speech, so we can find those impulse responses from this waveform.To find the fundamental periods we need to place pitch marks on the speech.Pitch marks are estimates of epochs, which are the moments of vocal fold closure.Pitch marking can be done automatically using methods which are beyond the scope of this video.Here's a short utterance and its pitch marks.It sounds like this: 'Nothing's impossible.'Let's take a closer look.If we look at this region, we see that the speech is transitioning from voiced to unvoiced.So what do we do there about the pitch marks?We still need to break this speech down into pitch periods, even when there is no fundamental frequency.In other words, we need to find analysis frames.So we'll just revert to a fixed frame rate - a fixed value of the fundamental period - and that's equivalent to just placing evenly-spaced pitch marks through the unvoiced regions.Zoom back out and look a different part of the utterance: the end, where the speech is finishing and we end up in silence.We'll see we also need to place pitch marks here, so that we can break this signal down into short parts.So we also need to place pitch marks in silence.In signal processing, silence is typically treated just like the rest of the signal.Now we've placed pitch marks on our signal.Aligning them precisely with the true epochs - which we don't have access to - is a little bit hard, although you can see that we can at least place one pitch mark in each fundamental period, and that's good enough.Now the vocal tract filter has a potentially infinite impulse response, due to vocal tract resonance.That means that one impulse response will generally not have decayed away to zero before the next one starts: they overlap.That's particularly obvious in this signal, which is speech from a female speaker.The fundamental period is about 4 ms, corresponding to an F0 of about 250 Hz.Quite clearly, the impulse response has not decayed to zero before the next impulse starts.The impulse responses overlap.Because the pitch marks might not be precisely at the true epoch locations, and because the impulse responses overlap, we can't naively cut this waveform into individual impulse responses.There's no place where we can do that.Instead, we'll remember something we learned earlier about short-term analysis.We will place an analysis frame - centred on each pitch mark - and apply a tapered window and use that to extract the pitch periods.We'll find each epoch; we'll place an analysis frame around it; we';l extract a pitch period like that.We'll do that for every pitch mark in the utterance to get a sequence of pitch periods.Typically, we make the duration of these twice the fundamental period: 2 x T0.Sometimes we just say 'two pitch periods'.These look very much like the overlapping frames of a typical short-term analysis technique.In fact, it's exactly the same.The only difference here is that we're placing the frames pitch-synchronously and we're varying their duration in proportion to the fundamental period: we're making it 2 x T0.These little pitch period building blocks capture only vocal tract filter information.These little pitch period building blocks are going to be now used to synthesise speech signals by concatenating them using overlap-add.Let's confirm then, that overlap-add of these pitch period does indeed reconstruct the original signal.These pitch periods were extracted using a very simple triangular window.So, if we overlap-add, everything adds back together correctly and we get almost the original signal back.Let's listen to the original whole utterance from which this fragment was taken: 'Nothing's impossible.'The reconstructed waveform from which the bottom fragment has come: 'Nothing's impossible.'If you listen carefully on headphones, you'll hear some small artefacts.But the waveform was reconstructed pretty well.I've reconstructed this waveform without making any modifications to it, just to prove that I can decompose a speech signal into pitch periods and put it back together again.This process is often called 'copy synthesis'.We've just seen a new form of signal processing, which is pitch-synchronous.It's essentially just the same as short-term analysis that we've seen before, except that we align the analysis frames to the fundamental periods of the signal and vary the analysis frame duration according to the fundamental period.This video is called 'Pitch period', but we had to actually generalise that concept a little bit because the impulse responses of the vocal tract typically overlap in natural speech signals.That makes it impossible to extract a single impulse response.The generalisation we made was to extract overlapping frames and apply a tapered window in a way that makes reconstruction of the signal possible by simply using overlap-add.This representation of the speech signal - as a sequence of pitch periods - is at the heart of the TD-PSOLA method, which can modify F0 and duration of speech signals in the time domain, using waveforms directly.We're also going to be able to understand the interaction of the source and filter in the time domain, which is a process known as convolution.
This video just has a plain transcript, not time-aligned to the videoWaveform generation is going to be achieved using a stored database of natural utterances, from which we can select diphones or sequences of diphones.Then we'll concatenate those waveform fragments.Each of them will have the correct pronunciation, but in general they won't have the right values of F0 and duration, that our front end has predicted.So we need to modify F0 and duration of recorded natural speech.We discovered that we can represent the vocal tract filter as its impulse response.We called that the 'pitch period'.We saw that we can extract these pitch periods from natural speech using pitch-synchronous overlapping analysis frames with a tapered window, a kind of short-term analysis.We're now going to combine that idea with the overlap-add technique for concatenating waveforms to create a general method, called TD-PSOLA, which can modify F0 and duration of recorded speech.The Time-Domain Pitch-Synchronous Overlap-and-Add algorithm operates in the time domain: on waveforms.This has a potential advantage over explicitly fitting a source-filter model, because we don't need to make any assumptions about the form of filter.For example, we don't need to decide how many coefficients to have in the difference equation.We could also avoid having to solve for those filter coefficients: that's a potentially error-prone process.TD-PSOLA uses pitch-synchronous short-term analysis to extract pitch periods from natural speech.Then it uses overlap-add to construct a modified waveform from those pitch period building blocks.That's not as powerful as explicitly using a source filter model though,.Because the filter response is represented in the time domain as its impulse response - the pitch periods - it's not in a form that we could easily modify, so TD-PSOLA can actually only modify F0 and duration.Those are both source features.It cannot modify the vocal tract filter: it will attempt to leave that unmodified.Here's a reminder of how we can break down a natural speech waveform into its pitch periods.Notice that they overlap in the original signal.That's essential because we're using a tapered window on each analysis frame.As we've seen before, we can overlap-add these pitch periods to reconstruct the original signal.The tapered window that we apply to each pitch period makes sure that they do add back up to the original signal where they overlap.Wherever these waveforms overlap, we just add them together, sample by sample.We'll reconstruct the original waveform very closely; not exactly, but very closely.This is just copy synthesis, but how about doing this?What do you think that will sound like?Pause the video.In the lower waveform, the fundamental period is larger than in the original waveform, so it will have a lower F0.So we'll perceive a lower pitch.The duration has also being changed though: it will be longer.But importantly, the individual pitch periods have not been changed.We're still playing back a sequence of impulse responses.So the vocal tract filter is the same and we'll hear the same phone.That's changing the fundamental period and therefore F0.I can also change duration by either duplicating or deleting pitch periods.So let's reduce the duration of this one.I'll lose this pitch period and overlap-and-add like this.Now I've got a signal with about the same duration as the original, but with only 6 fundamental periods where there used to be 7.I've reduced F0 without changing duration or changing the vocal tract filter.I can apply any combination of sliding the pitch periods a little closer together or a little further apart, with duplicating or deleting pitch periods, to gain independent control over F0 and duration.Let's see how that works.Let's increase F0.What are we going to do? slide them a little closer together to reduce the fundamental period.Let's decrease F0: slide them a little further apart - increase the fundamental period.Let's increase duration.By duplicating a pitch period, we'll make some space for it.Take one, copy it.We've now made the duration longer.I could repeat that; I could duplicate more and more of the pitch periods to make the duration longer and longer.Let's decrease duration.Pick a pitch period, lose it, and close the gap.I can increase or decrease F0, increase or decrease duration, and combine those operations any way I like.Let's put that all together and do speech synthesis!Finally, then here's the complete process of waveform generation.Here'a a database of diphone units.Each row is a natural utterance that I've recorded.Inside each of these diphones is a waveform fragment.I've segmented these utterances into diphones.I can select units from this database, and concatenate them to make a new word or utterance.I'm not actually going to explain how we decide between different alternative ways of constructing the new utterance here.That's a big problem to be solved in a longer course on speech synthesis.The method's actually called 'unit selection', for obvious reasons.Given this sequence of diphones from the database with the waveforms inside them, we now need to concatenate them.Each diphone contains a waveform.But it will be at whatever F0 and duration that the speaker said it at when we recorded the database.That won't match our desired values, predicted from the front end.So we need to apply TD-PSOLA to each diphone.Inside these diphones are waveforms.We're going to modify those waveforms using TD-PSOLA.Here's a fragment of waveform.We first break it down into its constituent pitch periods: replace it with these analysis frames, each of which is 2 fundamental periods long.Then we apply TD-PSOLA to match the predictions from the front end.Here, my front end predicted that F0 needs to actually be a little bit lower than what this speech was recorded at, and the duration needs to be a little bit longer.So I just spread the pitch periods out a bit and duplicate one to make the duration correct.This waveform now matches the predictions from the front end.I'll finish with some examples of TD-PSOLA operating.I'm going to just use a complete natural utterance as the starting point rather than concatenated diphones.Here it is: 'Nothing's impossible.'We can change F0, like this: 'Nothing's impossible.'Or like this: 'Nothing's impossible.'We can change duration; how about faster: 'Nothing's impossible.'Or slower: 'Nothing's impossible.'Those audio samples were actually made with my own very simple implementation of TD-PSOLA, and you'll hear a few artefacts, especially in the one that's slowed down.A more sophisticated implementation would reduce those quite a lot, but there are still limits to how much you can modify duration and F0 away from the original values before TD-PSOLA degrades the signal.That's the end of the material on waveform generation.But just before we finish, there's one more topic to cover.We've seen how the pitch period is a building block of speech, because it's the impulse response of the vocal tract filter.It's a view of the filter in the time domain.When we saw the source-filter model, we saw that we could combine the magnitude spectrum of the input signal with the magnitude frequency response of the filter to obtain the magnitude spectrum of the output signal.We combine them simply by multiplying them in the magnitude spectrum domain.In the time domain, the operation that combines the input signal with the filter's impulse response to produce the output signal is called 'convolution'.We need to understand the relationship between multiplication in the magnitude spectral domain and convolution in the time domain.
This video just has a plain transcript, not time-aligned to the videoWe spent some time developing an understanding of the source-filter model.We know that the filter can be described in several ways, including as its impulse response.That led us to the idea of the pitch period as a building block for manipulating speech.Now we're going to look at just how the source and filter combine in the time domain.This operation is called 'convolution'.First, a reminder of how the source-filter model operates, using the impulse response as our description of the filter.Here's the filter, as its impulse response.We need an input: an excitation signal.Let's start with just one impulse.If we input that to the filter, by definition, as output, we obtain the filter's impulse response.If we put in a sequence of two impulses, we get two impulse responses out.Put in three, get out three impulse responses, and so on.I like to think of this as each impulse exciting an impulse response and writing that into the output at the appropriate time.This impulse starts at 10 ms, and so it starts writing an impulse response into the output signal at 10 ms.This impulse writes its impulse response at its time, and so on.These impulses are quite widely spaced in time, and so each of these impulse responses has pretty much decayed to zero before we write the next impulse response in.That's a very easy case.If we decrease the fundamental period of the excitation, those impulse responses will be written into the output closer together in time, like this, or like this, and so on.Now let's use an impulse train as the excitation.The operation that combines these two waveforms to produce this waveform is called 'convolution'.Convolution is written with a star symbol.Let's do some convolution, whilst we inspect the magnitude spectrum of each of these signals.That's the magnitude spectrum of the excitation, of the filter, and of the output.The waveforms are sampled at 16 kHz, which means the Nyquist frequency will be 8 kHz.I've zoomed in the frequency axis so we can see a little bit more detail: I'm just plotting it up to 3 kHz.I'm going to increase the fundamental frequency of the excitation.I'd like you to watch, first of all, what happens to the magnitude spectrum of the excitation itself.Just watch this corner.That behaves as expected.We have harmonics spaced at the fundamental frequency and all integer multiples of that.So, as the fundamental frequency goes up, those harmonics get more widely spaced.I'm going to vary F0 again now, but this time I want you to look at the magnitude spectrum of the speech.I'm decreasing F0.What do we see?Well we saw those harmonics getting closer and closer together because they're multiples of the fundamental frequency.But the envelope remains constant because that's determined by the filter.If you're watching really closely, you might have seen the absolute level of this go up and down a small amount.That's simply because the amount of energy in the excitation signal varies with more and more impulses per second.That's not important here.It's the way that these two magnitude spectra combine that we're trying to understand.So I'll just vary F0 a few more times and have a look at the different magnitude spectra and try and understand how this and this combine to make this.Increasing F0 ... and decreasing F0.One more time: increasing it again.Let's try something else.Let's keep the excitation fixed and then let's vary the filter.That's a different filter ... and that's another one.I'll do that a few more times.Look at the magnitude spectrum of the output and see what varies there.Only the filter is changing.The excitation is constant.So, this time, the harmonic structure remained the same and the envelope followed that of the filter.We're getting a pretty good understanding, then, of how these two things combine to make the spectrum of the output.The two waveforms combine using convolution in the time domain.The Fourier transform converts convolution into multiplication.That means that the source and the filter can be combined by multiplying their magnitude spectra.That's something we mentioned in passing back when we were talking about the source-filter model.But we should be a bit more careful.Look very closely at the axes on the plots of the magnitude spectrum.You'll see that we're using a logarithmic axis.You can see that because the units are dB.Taking the logarithm converts multiplication into addition.So, in fact, the operation that combines the log magnitude spectrum of the excitation with the log magnitude spectrum of the filter is addition.That's a really elegant and simple way to combine source and filter in the frequency domain.We simply add together their log magnitude spectra!There's nothing in this diagram that requires this to be an impulse train and this to be the impulse response of a filter.They could be any two waveforms, and the operation of convolution is still defined.That means that this relationship is just generally true.Convolution of any two waveforms in the time domain is equivalent to summation of their log magnitude spectra.Given a speech signal like this, and its log magnitude spectrum, we quite often want to recover the source or the filter from that signal.For example, we'd like to recover this, which is the vocal tract frequency response (sometimes we use the more general idea of 'spectral envelope').That means doing this equation in reverse.Starting from this, we'd like to decompose it into a summation of two parts: one being the source, and one being the filter.That's going to be much easier in the log magnitude spectrum domain than in the time domain, because reversing a summation is much easier than undoing a convolution.We've seen that convolution in the time domain became multiplication in the magnitude spectral domain and then addition in the log magnitude spectral domain.This has applications in Automatic Speech Recognition, where we'll want only the vocal tract filter's frequency response to use as a feature for identifying which phone is being said.We'd like to get rid of the effects of the the source.We're going to develop a simple method to isolate the filter's frequency response without having to fit a source-filter model or find the fundamental periods.The method starts with the log magnitude spectrum and makes a further transformation into a new representation called the 'cepstrum', where the source and filter are very easy to separate.
Reading
Jurafsky & Martin – Section 8.4 – Diphone Waveform Synthesis
A simple way to generate a waveform is by concatenating speech units from a pre-recorded database. The database contains one recording of each required speech unit.
Jurafsky & Martin – Section 8.5 – Unit Selection (Waveform) Synthesis
A brief explanation. Worth reading before tackling the more substantial chapter in Taylor (Speech Synthesis course only).
Holmes & Holmes – Chapter 5 – Message synthesis from stored human speech components
Pitch-synchronous overlap-and-add (PSOLA) remains a key technique in speech signal processing.
Taylor – Section 12.7 – Pitch and epoch detection
Only an outline of the main approaches, with little technical detail. Useful as a summary of why these tasks are harder than you might think.
This lab session will give you a chance to get some extra help on your assignment. The following are suggestions on things you might like to prepare before the lab for feedback.
Get some writing advice
Bring a sample of your writing (150-200 words). Be ready to share it with Simon for feedback. It’s also good practice for you to get feedback on your writing from your peers, so feel free to do this in the lab or amongst yourselves at another time.
Generate some TTS error samples
Create some example synthetic speech, save the audio and spectrogram for your best example in each of the following categories, and come to the lab ready to explain to your tutor and classmates what the errors such as:
- Waveform generation mistakes, in which the front end did not make any mistakes, yet the synthetic waveform contains an audible problem.
- Synthetic speech in which there is a clearly visible join in the spectrogram, yet it is not audible.
- Mistakes in the TTS front-end
- Other things that sound weird!
You can use the speech zone forum on assignment 1 to ask for help. You might find some of your questions are already answered in previous posts.
Private
- You do not have permission to view this forum.
That’s the end of the Text-To-Speech part of the course. The last video of this module was a pointer forward into the Automatic Speech Recognition part of the course. It made it clear that all of our knowledge about speech signals, and in particular about separating the source and filter, will continue to be very useful.
What you should know
Note that Simon says in the videos that we don’t cover unit selection in this course, which is true for the videos but we do cover this in the lectures, readings and assignment.
- Diphone: why use diphones? how does this relate to coarticulation? what goes into a diphone database?
- Waveform concatenation, Overlap-add, Pitch period:
- What are potential issues for concatenating waveforms? i.e. when do we get ‘glitches’ and ‘pops’ ?
- Why are discontinuities at joins a problem?
- How does Overlap-add and pitch synchronous concatenation help
- TD-PSOLA
- What can you manipulate with TD-PSOLA?
- How does TD-PSOLA increase/decrease F0?
- How does TD-PSOLA increase/decrease duration?
- How does this relate to impulse responses? i.e. why doesn’t it change the actual phone/spectral envelope?
- Unit selection: Target and join costs (lecture and J&M 8.5) – we haven’t covered the Viterbi algorithm in Module 6, but it will come up again in the ASR modules for this course.
- Convolution : convolution in the time domain = multiplication in the frequency domain (i.e. see the application of filters in the frequency domain – module 4, e.g. low/band/high pass filters). You should aim to understand this at a conceptual level.
- Connected speech/citation speech:
- identify examples of connected speech processes: assimilation, lenition, deletion, vowel reduction, as discussed in the lectures/videos in reference to potential rules helping us to generate correct pronunciations.
Key Terms
- diphone, diphone database
- concatenation
- concatenative synthesis
- waveform, waveform generation
- diphone synthesis
- unit selection
- coarticulation
- overlap-add
- pitch period
- TD-PSOLA
- discontinuity
- join, join cost
- target, target cost
- convolution
- connected speech
- assimilation
- lenition
- deletion
- vowel reduction