You are here:Home Courses Speech Processing Module 3 – Digital Speech Signals

Module 3 – Digital Speech Signals

What are spectrograms really? An introduction to Digital Signal Processing and the Discrete Fourier Transform
Log in

Remember to watch the module videos before the Thursday Lecture! 

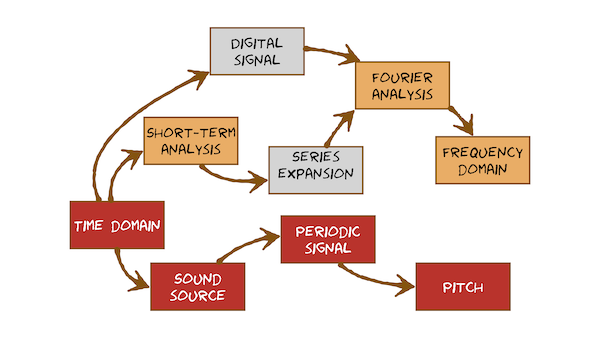
In this module we will look at how the speech produced by a physical system is captured as a digital signal, i.e., how it goes from a pressure wave to a sequence of 0s and 1s on your computer. We will see how engineering decisions affects what we can capture and what sort of analysis we can do. The most important constraint we will come up against is sampling rate. Given a digitized waveform, we then introduce the Discrete Fourier Transform (DFT) as a method of mapping from the time domain to the frequency domain. The DFT is what allows us to create spectrograms. We’ll see that the frequency domain is a much more more convenient place to do speech processing than the time domain. But, again, the fact that we’re working with digital signals determines what we actually get out of a spectrogram.

The Discrete Fourier Transform (and signal processing in general) uses sine and cosine functions a lot. If you haven’t thought about sines and cosines for a while (SOH CAH TOA ring any bells?), you might also want to brush up on some trigonometry and vectors:

We won’t ask you to derive the DFT equation etc, but knowing a bit more maths will help develop your intuitive understanding of what’s going on here.

Here’s what you are going to learn in this module’s videos:

Lecture Slides

Lecture 3 slides (google slides) [updated 1/10/2024 ]

 

Total video to watch in this section: 37 minutes.

To do speech processing with a computer, we need to convert sound first to an analogue electrical signal, and then to a digital representation of that signal.

This video just has a plain transcript, not time-aligned to the videoThe very first step in processing speech is to capture the signal in the time domain and create a digital version of it in our computer.
Here's a microphone being used to measure a sound wave.
The output of the microphone is an analogue voltage.
We need to convert that to a digital signal so we can both store it and then manipulate it with a computer.
How do we convert an analogue signal to a digital one?
In other words, what is happening here?
In the analogue domain, things move smoothly and continuously.
Look at the hands on this analogue watch, for example.
It tells the time with infinite precision, not just to the nearest second.
But in stark contrast, in the digital domain, there are a fixed number of values that something can take: there is finite precision.
So this digital clock does only tell the time to the nearest second.
It has made time discrete, and that's an approximation of reality.
So why cannot computers store analogue values?
It's because computers only store binary numbers, nothing else.
Everything has to be represented as a binary number.
It has to be placed in the finite amount of storage available inside the computer.
So, for our waveform, there are two implications of that.
1) we have to represent the amplitude of the waveform with some fixed precision, because it's going to have to be a binary number.
2) we can only store that amplitude a finite number of times per second, otherwise we would need infinite storage.
Start by considering these binary numbers.
With one bit, we have two possible values.
With two bits, we get four values.
With three bits, we get eight values, and so on.
The amplitude of our waveform has to be stored as a binary number.
But let's first consider making time digital: making time discrete.
Let's zoom into this speech waveform.
It appears to be smooth and continuous, but zoom in some more, and keep zooming in, and eventually we'll see that this waveform has discrete samples.
The line joining up the points on this plot is just to make it pretty; it's to help you see the waveform.
In reality, the amplitude is only stored at these fixed time intervals.
Each point in this plot is a sample of the waveform.
Let's first decide how frequently we should sample the waveform.
I'm drawing this sine wave in the usual way with a line joining up the individual samples, and you can't see those samples, so I'll put a point on each sample.
This is sampled so frequently, we can barely see the individual points.
But let's reduce the sampling rate.
There are fewer samples per second, and now you can see the individual samples.
Remember, the line is just a visual aid: the waveform's value is defined only at those sample points.
Keep reducing the sampling rate, and that's as far as we can go.
If we go any lower than this, we won't be able to store the sine wave.
It won't go up and down once per cycle
We have discovered that, to store a particular frequency, we need to have a least two samples per cycle of the waveform.
Another way of saying that is: the highest frequency that we can capture is half of the sampling frequency.
That's a very special value, so special it has a name, and it's called the Nyquist frequency.
A digital waveform cannot contain any frequencies above the Nyquist frequency, and the Nyquist frequency is just half the sampling frequency.
But what would happen then, if we did try to sample a signal whose frequency is higher than the Nyquist frequency?
Here's a sine wave and let's take samples of it less often than the Nyquist frequency.
To make it easier to see what's happening, I'm going to draw a line between these points.
This waveform doesn't look anything like the original sine wave!
We've created a new signal that's definitely not a faithful representation of the sine wave
This effect of creating a new frequency, which is related to the original signal and to the sampling frequency, is called aliasing.
It's something to be avoided!
Whenever we sample on analogue signal, we must first remove all frequencies above the Nyquist frequency, otherwise we'll get aliasing.
We must also do that if we take a digital signal like this one on reduce its sampling frequency.
Let's listen to the effect of sampling frequency.
These are all correctly-sampled signals.
We've removed everything below the Nyquist frequency before changing the sampling rate.
For speech, a sampling rate of 16 kHz is adequate, and that sounds fine.
Let's listen to reducing the sampling rate.
We've lost some of the high frequencies.
We've lost even more of the high frequencies
And even more of them.
Even at this very low sampling rate of 4 kHz, speech is still intelligible.
We can still perceive pitch, but we've lost some of the sounds.
The fricatives are starting to go because they're at higher frequencies.
Hopefully, you've noticed that I've been using a few different terms interchangeably.
I've said 'sampling frequency', I've said 'sampling rate', or perhaps just 'sample rate'.
Those are all interchangeable terms that mean the same thing.
So we've dealt with making time discrete.
That's the most important decision: to choose the sampling rate.
For Automatic Speech Recognition, 16 kHz will be just fine, but for Speech Synthesis typically we'd use a higher sampling rate than that.
Let's turn over to making amplitude digital or amplitude discrete.
Here's waveform that I've sampled: I've chosen the sampling rate and we have samples evenly spaced in time.
Now I've got to write down the value of each sample, and I've got to write that down as a binary number, and that means I have to choose how many bits to use for that binary number.
Maybe I'll choose to use two bits, and that will give me four levels.
So each one of these samples would just have to be stored as the nearest available value: that's called quantisation.
We need to choose a bit depth, but there is a very common value, and that's 16 bits per sample, and that gives us 2 to the power 16 available discrete levels.
We have to use them to span both the negative and positive parts of the amplitude axis.
So just sometimes in some pieces of software, you might see the amplitude axis labelled with a sample value.
That would go from -32,768 up to +32,767 because one of the values has to be zero.
The number of bits used to store each sample is called the bit depth.
Let's listen to the effect of changing the bit depth, and in particular reducing it from this most common value of 16 bits to some smaller value.
That sounds absolutely fine.
That sounds pretty good.
Listen on headphones, and you might hear small differences.
That sounds pretty nasty.
Brace yourself: we're going down to two bits...
Pretty horrible!
It's quite different though to the effect of changing the sampling frequency.
Reducing the bit depth is like adding noise to the original signal.
In fact, it is adding noise to the original signal because each sample has to be moved up or down to the nearest possible available value.
With fewer bits, there are fewer values and therefore more noise is introduced, noise being the error between the quantised signal and the original.
Very rarely do we bother reducing the bit depth, and we stick with 16 bits for almost everything.
With two bits, we can actually see those values.
If we look carefully on this waveform, we can see there are only four different values within the waveform.
Those relate to the four possible values we get with two binary bits.
We started in the time domain, with an analogue signal provided by a microphone.
That's an analogue of the pressure variation measured by that microphone.
But now we have a digital version of that signal.
Going digital means that we can now do all sorts of sophisticated, exciting operations on the signal using a computer.
That's extremely convenient.
But you must always be aware that the digital signal has limitations.
We have made approximations.
The most important limitation to always bear in mind is the sampling frequency.
That's something we might want to vary, depending on our application.
Bit depth is also something to bear in mind, but in practical terms and for our purposes, we're just going to use a universal bit depth of 16.
That's plenty: the quantisation noise is negligible, and we won't generally be varying that value.
Now we have a digital signal, we're ready to do some speech processing.
One of the most important processes is to use Fourier analysis to take us from the time domain to the frequency domain.

Log in if you want to mark this as completed
Because speech sounds change over time, we need to analyse only short regions of the signal. We convert the speech signal into a sequence of frames.

This video just has a plain transcript, not time-aligned to the videoShort-term analysis is the first step that takes us out of the time domain and into some other domain, such as the frequency domain.
Here's a spoken word.
Clearly, its properties vary over time.
The amplitude varies.
Or, for example, some parts are voiced: this is voiced, this is voiced.
But other parts are not: this part's unvoiced.
Apart from measuring the total duration, it makes no sense to analyse any other properties of a whole utterance.
For example, F0 doesn't just vary over time, it only exists in the voiced regions and doesn't even exist in the unvoiced parts.
Because short-term analysis is the first step, in general we need to perform it without knowing anything about the waveform.
For example, in Automatic Speech Recognition, the analysis takes place before we know what words have been spoken.
So we can't do the following: we can't segment the speech into linguistically-meaningful units and then perform some specific analysis, for example, on this voiced fricative, or this vowel, or this unvoiced fricative.
Rather, we need to use a general-purpose method, which doesn't require any knowledge of the contents of the signal.
To do that, we're going to just divide the signal into uniform regions and analyse each one separately.
These regions are called frames and they have a fixed duration, and that duration is something we have to choose.
Here's the plan: we'll take our whole utterance and we'll zoom into some shorter region of that and perform some analysis.
Then we shift forward in time, analyse that region, then move forward again, analyse that region, and so on, working from the start of the utterance to the end in some fixed steps.
The first thing to decide is how much waveform to analyse at any one time.
The waveform in front of you clearly substantially varies its properties, so we need a shorter region than that.
We'll define a frame of the waveform first by choosing a window function and then multiplying the waveform by this window function.
My window here is the simplest possible one: a rectangular window that is zero everywhere except within the frame I wish to analyse, where it's got a value of one.
We multiply the two, sample by sample, and obtain a frame of waveform that's - if you like - "cut out" of the whole utterance.
This cut-out fragment of waveform is called a frame.
We're then going to move forward a little bit in time and cut out another frame for analysis.
So here's the process:
Cut out of frame of waveform: that's ready for some subsequent analysis.
Move forward some fixed amount in time, cut out another frame, and so on to get a sequence of frames cut out of this waveform.
That's done simply by sliding the window function across the waveform.
Let's take a closer look at one frame of the waveform.
Because I've used the simplest possible rectangular window, we've accidentally introduced something into the signal that wasn't there in the original.
That's the sudden changes at the edge of the signal.
These are artefacts: that means something we introduced by our processing, that's not part of the original signal.
If we analysed this signal we'd not only be analysing the speech but also those artefacts.
So we don't generally use rectangular window functions because these artefacts are bad, but rather we use tapered windows.
When we cut out a frame, it doesn't look like this, but it's cut out with a window function that tapers towards the edges.
Think of that as a fade-in and a fade-out.
That gives us a frame of waveform that looks like this: it doesn't have those sudden discontinuities at the edges.
Here's the complete process of extracting frames from a longer waveform using a tapered window.
Typical values for speech will be a frame duration of 25 ms and a frame shift off something less than that, and that's because we're using these tapered windows.
To avoid losing any waveform, we need to overlap the analysis frames.
So, we'll extract one frame, then the next, and the next, each one having a duration of 25 ms and each one being 10 ms further on in time than the previous one.
We've converted our complete utterance into a sequence of frames.
This representation - the sequence of frames - is the basis for almost every possible subsequent analysis that we might perform on a speech signal, whether that's estimating F0 or extracting features for Automatic Speech Recognition.
With a speech utterance broken down now into a sequence of frames, we're ready to actually do some analysis.
Our first, and most important, destination is the frequency domain, which escapes many of the limitations of doing analysis directly in the time domain.
Now, to get to the frequency domain, we're going to use Fourier analysis and that will be introduced actually in two stages.
First we'll have the rather abstract concept of Series Expansion, and then we'll use that to explain Fourier analysis itself.

Log in if you want to mark this as completed
Speech is hard to analyse directly in the time domain. So we need to convert it to the frequency domain using Fourier analysis, which is a special case of series expansion.

This video just has a plain transcript, not time-aligned to the videoBecause speech changes over time, we've already realised that we need to analyse it in the short-term.
We need to break it into frames and perform analysis frame by frame.
One of the most important analyses is to get into the frequency domain.
We're going to use Fourier analysis to do that, but we're going to introduce that in two stages.
So the first topic is actually going to seem a little abstract.
There's a reason for introducing series expansion as an abstract concept, and that's because it has several different applications.
The most important of those is Fourier analysis, but there will be others.
Here's a speech-like signal that we'd like to analyse.
So maybe we should really say what 'analyse' means.
Well, how about a concrete example?
I'd like to know what this complicated waveform is 'made from'.
One way to express that is to say that it's a sum of very simple waves.
So we're going to expand it into a summation of the simplest possible waves.
That's what series expansion means.
For the purpose of the illustrations here, I'm just going to take a single pitch period of this waveform.
That's just going to make the pictures look a little simpler.
But actually everything we're going to say applies to any waveform.
It's not restricted to a single pitch period.
I'm going to express this waveform as a sum of simple functions.
Those are called basis functions and as the basis function I'm going to use the simplest possible periodic signal there is: the sine wave.
So let's try making this complex wave by adding together sine waves.
This doesn't look much like a sine wave, so maybe you think that's impossible.
Not at all!
We could make any complex wave by adding together sine waves.
I've written some equations here.
I've written that the complex wave is approximately equal to something that I'm going to define.
Let's try using just one sine wave to approximate this.
Try the sine wave here, and the result is not that close to the original.
So let's try adding a second basis function at a higher frequency.
Here it is: now if we add those two things together, we got a little closer
I'll add a third basis function at a higher frequency still, and we get a little closer still, and the fourth one, and we get really quite close to the original.
It's not precisely the same, but it's very close.
I've only used four sine waves there.
The first sine wave has the longest possible fundamental period: it makes one cycle in the analysis window.
The second one makes two cycles.
The third one makes three cycles, then four cycles and so on.
So they form a series.
Now, I can keep adding terms to my summation to get as close as I want to the original signal.
So let's keep going.
I'm not going to show every term because there's a lot of them.
But we keep adding terms and eventually, by adding enough terms going up to a high enough frequency, we will reconstruct exactly our original signal.
Now we're not just approximating the signal, it is actually now equal.
Theoretically, if this was all happening with analogue signals, I might need to add together an infinite number of terms to get exactly the original signal.
But these are digital signals.
That means that this analysis frame has a finite number of samples in it.
This waveform is sampled at 16 kHz and it lasts 0.01 s.
That means there are 160 samples in the analysis frame.
Because there's a finite amount of information, I only need a finite number of basis functions to exactly reconstruct it.
Another way of saying that is that these basis functions are also digital signals, and the highest possible frequency one is the one at the Nyquist frequency
So if I sum up basis functions all the way up to that highest possible frequency one, I will exactly reconstruct my original signal.
So what exactly have we achieved by doing this?
We've expressed the complex wave on the left as a sum of basis functions, each of which is a very simple function: it's a sine wave, at increasing frequency.
We've had to add together a very specific amount of each of those basis functions to make that reconstruction.
We need 0.1 of this one and 0.15 of this one and 0.25 of this one and 0.2 of this one and just a little bit of this one, and whatever the terms in between might be, to exactly reconstruct our signal.
This set of coefficients exactly characterises the original signal, for a fixed set of basis functions.
Because we can choose how many terms we have in the series - we can go as far as we like down the series but then stop any where we like - we actually get to choose how closely we represent the original signal.
Perhaps all of this fine detail on the waveform is not interesting: it's not useful information.
Maybe it's just noise, and we'd like to have a representation of this signal that removes that noise.
Well, series expansion gives us a principled way to do that.
We can just stop adding terms.
This signal might be a noisy signal and this signal is a denoised version of that signal.
It removes the irrelevant information (if that's what we think it is).
The main point of understanding series expansion is as the basis of Fourier analysis, which transforms a time domain signal into its frequency domain counterpart.
But we will find other uses for series expansion, such as the one we just saw, of truncation to remove unnecessary detail from a signal.
What we learned here is not restricted to only analysing waveforms.
There's nothing in what we did that relies on the horizontal axis being labelled with time: it could be labelled with anything else.
Fourier analysis will then do what we've been trying to do for some time: to get us from the time domain into the frequency domain where we can do some much more powerful analysis and modelling of speech signals.

Log in if you want to mark this as completed
We can express any signal as a sum of sine waves that form a series. This takes us from the time domain to the frequency domain.

This video just has a plain transcript, not time-aligned to the videoWe're now going to use a series expansion approach to get from a digital signal in the time domain to its frequency domain representation.
All the signals are digital.
We understand how series expansion works, in a rather abstract way.
We're now going to make that concrete, as Fourier analysis.
Let's just recap series expansion.
We saw how it's possible to express a complex wave, for example this one, as a sum of simple basis functions.
We wrote the complex wave as equal to a weighted sum of sine waves.
Let's write that out a little more correctly.
We have some coefficient - or a weight - times a basis function.
These basis functions have a unit amplitude, so they're scaled by their coefficient and then added together.
We add some number of basis functions in a series, to exactly reconstruct the signal we're analysing.
So this is the analysis: the summation of basis functions weighted by coefficients.
Notice how those basis functions - those sine waves - are a series.
Each one has one more cycle in the analysis frame than the previous one.
These are coefficients and we now need to think about how to find those coefficients, given only the signal being analysed and some pre-specified set of basis functions.
Here is a series of basis functions: just the first four to start with.
I want you to write down their frequencies and work out the relationship between them.
Pause the video.
The duration of the analysis window is 0.01 s.
The lowest frequency basis function makes one cycle in that time, meaning it has a frequency of 100 Hz.
I'm going to start writing units correctly: we put a space between the number and the units.
The second one makes two cycles in the same amount of time, so it must have a frequency of 200 Hz.
The next one makes three cycles, that's 300 Hz.
And 400 Hz.
I hope you got those values.
It's just an equally-spaced series of sine waves, starting with the lowest frequency and then all the multiples of that, evenly spaced.
If I tell you now that the sampling rate is 16 kHz, there's lots more basis functions to go.
What's the highest frequency basis function that you can have?
Pause the video.
Well, we know from digital signals that the highest possible frequency we can represent is at the Nyquist frequency, which is simply half the sampling frequency.
The Nyquist frequency here would be 8 kHz.
We'd better zoom in so we can actually see that.
There we go: this waveform here has a frequency of 8 kHz.
We can't go any higher than that.
Fourier analysis simply means finding the coefficients of the basis functions.
We need somewhere to record the results of our analysis, so I've made some axes on the right.
This horizontal axis is going to be the frequency of the basis function.
Because we're going to go up to a basis function at 8000 Hz (that's 8 kHz), I'll give that units of kHz.
On the vertical axis, I'm going to write the value of the coefficient.
I'm going to call that magnitude.
Here's the lowest frequency basis function.
It's the one at 100 Hz.
So I'm going to plot on the right at 100 hertz (that's 0.1 kHz, of course) how much of this basis function we need to use to reconstruct our signal.
How do we actually work that amount out?
We're going to look at the similarity between the basis function and the signal being analysed.
That's a quantity known as correlation.
That's achieved simply by multiplying the two signals sample by sample.
So we multiply this sample by this sample and add it to this sample by this sample, and this sample by this sample, and so on and add all of that up.
That will give us a large value when the two signals are very similar.
In this example, if I do that for this lowest frequency basis function, I'm going to get a value 0.1.
Let's put some scale on this.
Then I'll do that for the next basis function
That's going to be at 0.2 kHz and I do the correlation and I find out that I need 0.15 of this one.
Then I do the next one, 0.3 kHz, and I find that I need 0.25 of this one.
Then the next one, 0.4 kHz, and I find that I need 0.2 of that one; and so on.
I've plotted a function on the right.
Let's just join the dots to make it easier to see.
This is called the spectrum.
It's the amount of energy in our original signal at each of the frequencies of the basis functions.
We now need to talk about a technical but essential property of Fourier analysis, where the basis functions are sine waves (in other words pure tones).
They contain energy at one and only one frequency.
That means that any pair of sine waves in our series are orthogonal.
Let's see what that means.
Take a pair of basis functions: any pair.
I'll take the first two, and work out the correlation between these two signals.
So multiply them sample by sample: this one by this one, this one by this one, and so on, and work out that sum.
For this pair, it will always be zero.
We can see that simply by symmetry.
These two signals are orthogonal.
There is no energy at this frequency contained in this signal, and vice versa.
The same thing will happen for any pair.
The correlation between them is zero.
There is no energy at this frequency in this waveform, and vice versa.
This property of orthogonality between the basis functions means that when we decompose a signal into a weighted sum of these basis functions, there is a unique solution to that.
In other words, there is only one set of coefficients that works.
That uniqueness is very important.
It means that there's same information in the set of coefficients as there is in the original signal.
It's also easy to invert this transform.
We could just take the weighted sum of basis functions and get back the original signal perfectly.
So Fourier analysis, then, is perfectly invertible, and gives us a unique solution.
We could go from the time domain to the frequency domain, and back to the time domain as many times as we like, and we lose no information.
We've covered, then, the essential properties of Fourier analysis.
It uses sine waves as the basis function.
There is a series of those from the lowest frequency one (and that frequency will be determined by the duration of the analysis window) up to the highest frequency one (and that will be determined by the Nyquist frequency).
We said Fourier 'analysis', but this conversion from time domain to frequency domain is often called a 'transform'.
So from now on we'll more likely say the 'Fourier transform'.
The Fourier transform is what's going to now get us into the frequency domain.
That's one of the most powerful and widely used transformations in speech processing.
We do a lot more processing in the frequency domain than we ever do in the time domain.

Log in if you want to mark this as completed
We complete our understanding of Fourier analysis with a look at the phase of the component sine waves, and the effect of changing the analysis frame duration.

This video just has a plain transcript, not time-aligned to the videoYou already know the essential features of Fourier analysis, but we've glossed over a little detail called phase.
So we need to now clarify that, as well as then using Fourier analysis to transform any time domain signal into its spectrum: more correctly, its magnitude spectrum as we're going to see.
From now on will be calling this the Fourier transform.
We take a time domain signal.
We break it into short analysis frames.
On each of those, we perform a series expansion.
The series of basis functions are made of sine waves of increasing frequency.
That is Fourier analysis and that gets us now into the frequency domain.
In the general case, we need to worry not just about the magnitude of each of the basis functions, but also something called phase.
Consider this example here.
Look at the waveform on the left.
Look at the basis functions on the right.
See if you can come up with a set of coefficients that would work.
Well, fairly obviously you cannot, because all the basis functions are zero at time zero.
We're trying to construct a non-zero value at time zero, and there are no weights in the world that will give us that.
So there's something missing here.
This diagram is currently untrue, but I can make it true very easily by just shifting the phase of the basis function on the right.
Now the diagram is true!
Phase is simply the point in the cycle where the waveform starts.
Another way to think about it is that we can slide the basis functions left and right in time.
So when we are performing Fourier analysis, we don't just need to calculate the magnitude of each of the basis functions, but also their phase.
But does phase matter?
I mean, what does phase mean?
Is it useful for anything?
Here I've summed together four sine waves with this set of coefficients to make a waveform that speech-like.
There's one period of it on the right.
I'm going to play you a longer section of that signal.
OK, it's obviously not real speech!
I mean, I just made it by adding together these sine waves with those coefficients.
But it's got some of the essential properties of speech.
For example, it's got a perceptible pitch, and it's not a pure tone.
I'm going to use the same set of coefficients, but I'm going to change the phases of the basis functions.
So, exactly the same basis functions, they just start at different points in their cycle.
The resulting signal now looks very different to the original signal.
Do you think it's going to sound different?
Well, let's find out.
No, it sounds exactly the same to me.
Our hearing is simply not sensitive to this phase difference.
So for the time being, we're just going to say that phase is not particularly interesting.
Our analysis of speech will only need to worry about the magnitudes.
In other words, these are the important parts.
These phases - exactly where these waveforms start in their cycle - is a lot less important.
In fact, we're just going to neglect the phase from now on.
If we plot just those coefficients, we get the spectrum, and that's what I've done here.
On the left is the original signal, and its magnitude spectrum.
On the right is the signal with different phases, but the same magnitudes: its magnitude spectrum is identical.
We'll very often hear this called the spectrum, but more correctly we should always say the 'magnitude spectrum' to make it clear that we've discarded the phase information.
Something else that's very important that we can learn from this picture is that in the time domain two signals might look very different, but in the magnitude spectrum domain, they're the same.
Now that's telling us that the time domain might not be the best way to analyse speech signals.
The magnitude spectrum is the right place.
Because the amount of energy at different frequencies in speech can vary a lot - it's got a very wide range - the vertical axis of a magnitude spectrum is normally written on a log scale and we give it units of decibels.
This is a logarithmic scale.
But like the waveform, it's uncalibrated because, for example, we don't know how sensitive the microphone was.
It doesn't really matter because it's all about the relative amount of energy at each frequency, not the absolute value.
Back to the basis sine waves for a moment.
They start from the lowest possible frequency, with just one cycle fitting the analysis frame, and they go all the way up to the highest possible frequency, which is the Nyquist frequency.
They're spaced equally and the spacing is equal to the lowest frequency.
Here it's 100 Hz.
It's 100 Hz because the analysis frame is 1/100th of a second.
So what happens if we make the analysis frame longer?
Imagine we analyse a longer section of speech than 1/100th of a second.
Have a think about what happens to the set of basis functions.
Pause the video.
Well, if we've got a longer analysis window, that means that the lowest frequency sine wave that fits into it with exactly one cycle will be at a lower frequency, so this frequency will be lower.
We know that the series are equally spaced at that frequency, so they'll all go lower and they'll be more closely spaced.
But we also know that the highest frequency one is always at the Nyquist frequency.
So if the lowest frequency basis function is of a lower frequency and they're more closely spaced, then we'll just have more basis functions fitting into the range up to the Nyquist frequency.
A longer analysis frame means more basis functions.
This will be easier to understand if we see it working in practise.
Here I've got a relatively short analysis frame and on the right, I'm showing its magnitude spectrum: that's calculated automatically with the Fourier transform.
Let's see what happens as the analysis frame gets larger.
Can you see how a bit more detail appeared in the magnitude spectrum?
Let's go out some more, and even more detail appeared.
In fact there's so much detail, we can't really see it now.
So what I'm going to do is I'm actually going to just show you a part of the frequency axis: a zoomed-in part.
The spectrum still goes up to the Nyquist frequency, but I'm just going to show you the lower part of that, so we see more detail.
So there's the very short analysis frame and its magnitude spectrum.
Zoom out a bit and a bit more detail appears in the magnitude spectrum.
We make the analysis frame longer still, and we get a lot more detail in the magnitude spectrum.
So a longer analysis frame means that we have more components added together (more basis functions), therefore more coefficients.
Remember that the coefficients are just spaced evenly along the frequency axis up to the Nyquist frequency, and so we're just going to get them closer together as we make the analysis frame longer, so we see more and more detail in the magnitude spectrum.
Analysing more signal gives us more detail on the spectrum.
This sounds like a good thing, but of course that spectrum is for the entire analysis frame.
It's effectively the average composition of a signal within the frame.
So a larger analysis frame means we're able to be less precise about where in time that analysis applies to, so we get lower time resolution.
So it's going to be a trade-off.
Like in all of engineering, we have to make a choice.
We have to choose our analysis frame to suit the purpose of the analysis.
It's a design decision.
The next steps involve finding, in the frequency domain, some evidence of the periodity in the speech signal: the harmonics.
But that will only be half the story, because we haven't yet thought about what the vocal tract does to that sound source.
Our first clue to that will come from the spectral envelope.
So we're going to look at two different properties in the frequency domain.
We see both of them together in the magnitude spectrum, one being the spectral envelope, and the other being the harmonics.

Log in if you want to mark this as completed

We’re moving to the Wayland (2019) textbook for modules 3 and 4, though the material will presented in a somewhat different order. We’re focusing on digital signals this week, but you might also want to look at Chapter 6 “Basic Acoustics” this week (it’s also the module 4 essential reading, so if you read it this week you’ll be ahead for that. If you don’t get to it until next week, don’t worry!). You will have already got some of this from the previous module readings (e.g. source-filter model) but we’ll go into more details in the next weeks.

The background reading on digital signals is fairly high level.  If you want to see more maths, you can look at the extension materials in the labs or the references mentioned there.

Reading

Wayland (Phonetics) – Chapter 7 – Digital Signal Processing

An intuitive introduction to acoustics digital signal processing

Wayland (Phonetics) – Chapter 6 – Basic Acoustics

A concise introduction to acoustics: sounds, resonance, and the source-filter theory

Schaedler – Seeing Circles, Sines and Signals

A very nice concise primer on the basic components of digital signal processing with great visual demonstrations.

Handbook of phonetic sciences – Ch 20 – Intro to Signal Processing for Speech (Sections 1-5)

Written for a non-technical audience, this gently introduces some key concepts in speech signal processing. Read sections 1-5 (up to and including 'Fourier Analysis').

Lyons – Understanding Digital Signal Processing

A great introduction to digital signal processing, including the maths!

This is SIGNALS lab is about taking signals from the time domain into the frequency domain and will focus on analysing digital signals with the Discrete Fourier Transform.

The signal processing labs will use Jupyter notebooks: a combination of Python code and notes that you access using a web browser.

You can find a github repository for the signals notebooks here: https://github.com/laic/uoe_speech_processing_course. You can find the notebooks for this module in that repository under signals/signals-lab-1.

Getting started with Jupyter Notebooks

Don’t worry if you don’t know any Python – this is not a formal requirement of the course, and you’ll learn what you need simply by doing the exercises. You can run the notebooks on your personal computer but we’d suggest that you use Edina Notable service You can access from the Learn site for this course. You can also use direct login if you are already logged into Learn.

  1. Use a web browser to open the instructions; read them through once before doing anything else.
  2. The default would be to then follow “Run the notebooks online using Edina Noteable“.
    • If you feel  confident or already know Jupyter notebooks, you could also run the notebooks on your own computer: follow “Running Jupyter Notebooks on your computer“
    • This involves installing Python 3.9 and Miniconda on your own computer, but these are things you will find useful more generally in the future too. This uses around 1 GB of disk space.
  3. Once you have succeeded, finish this task by completing Section 4 of the Jupyter notebook sp-m0-how-to-start

You can always ask the tutors in the lab sessions for help with setting things up!

For further technical support in setting up Jupyter Notebooks, use this forum.

Please note, the material in notebooks is to support your learning. Nothing related to the code specifically is directly assessed (though the concepts in the notebooks marked essential may be). You don’t need to know Python to do this course, though MSc SLP students will need to know Python for many other courses so getting a more bit of practise/exposure definitely doesn’t hurt!

Notebooks for this module

First have a look at the guide to the signals notebooks. You can just look in the signals directory once you’re downloaded your own copy of the notebook repository.

After that, there is one essential notebook to work through:

  1. Digital Speech Signals

The lab is setup so the focus is mostly on changing small bits of existing code. However, if you are already experienced with python and numpy/matplotlib/librosa, you may want to try coding up some of the steps we take yourself.

Those notebooks are relatively light on the maths behind these technologies, but there are also some extension materials in signals-lab-1/extension directory that go into the details more.

Answers/Notes for Module 3 lab










Module 3 gave an introduction to digital signal processing. We hope you can now see the connection between articulatory and acoustic phonetics, and how we might use our knowledge of this to start building computational models for the analysis of speech. Now is a good time to think about what computational models would need to capture in order to characterise different speech sounds, e.g. properties of vowels (like formants), and consonants (like frication or bursts).

The fact that we have to digitize the speech signal and do short term analysis on speech results in specific design decisions, e.g. the sampling rate, window size. We can attempt to get a ‘better’ view of the spectral characteristics of speech by engineering the size and type of windows we use as inputs to the Discrete Fourier Transform (DFT).

Both signal processing and acoustic phonetics are massive fields. We do not except you to show mastery of both in only a few weeks! For the purposes of this course, you should be able to:

  • Explain how sampling rate determines which frequencies can be captured in a digital speech signal, i.e., What is aliasing? What is the Nyquist Frequency?
  • Explain how the DFT is used to generate a spectrogram
  • Describe what the output of the DFT is, what the magnitude and phase spectrums are, and why we only visualize the first half of the magnitude spectrum in a a spectrogram.
  • Describe how input size and sampling rate determine which frequencies can be analysed in a spectrogram
  • Describe what spectral leakage is and when it occurs
  • Describe how window shape can affect the shape of the magnitude spectrum

It’s out of scope for this class, but for real applications we also have to consider how fast our algorithms are. In general, you will be using the Fast Fourier Transform (FFT), an implementation of the DFT that allows us to make use of the certain repetitions/overlaps in how we calculate the separate DFT outputs to get the results faster. The python numpy FFT function is used in the module 3 lab, notebook 1, to show you what to expect if you try an off-the-shelf DFT implementation. The time gains aren’t really noticeable for the small examples used in the the lab notebooks, but when dealing with real world data, the optimizations of the FFT make a big difference. In general, you will see that there are many ways to solve the same problem. We’ll come back to this later in the course, when we look at an algorithmic method called dynamic programming.

What you should know

Some more detailed notes on what’s examinable from this module:

Digital Signals:

  • Explain how bit depth (i.e. quantisation) effects the quality of a digitized speech signal
  • Sampling rate: Explain how sampling rate determines which frequencies can be captured in a digital speech signal, i.e. how this relates to:
    • Aliasing
    • Nyquist Frequency

Short Term analysis: Why do we do short term analysis on speech (i.e. windowing)?

Series expansion, Fourier analysis, frequency domain:

  • What do we uses the Discrete Fourier Transform for?
    • i.e. mapping from the ime domain to Frequency domain
    • Interpret the DFT as a series expansion of a complex waveform
  • Describe what the output of the DFT is:
    • If the input is a sequence length N, how many outputs are there?
    • What do the magnitude and phase spectrums represent? What’s on the x and y axes?
    • Why do we only visualize the first half of the magnitude spectrum in a a spectrogram? (i.e. link to aliasing)
  • Describe how input size and sampling rate determine which frequencies can be analysed in a spectrogram:
    • Calculate what frequencies are represented in the DFT output
    • When does spectral leakage occur? (see Lecture, lab notebook)
  • Describe how window shape can affect the shape of the magnitude spectrum, i.e. why do we want a tapered window?
  • What’s the relationship between the DFT and what we actually see in a spectrogram?
  • What’s the difference between a narrow versus a wide band spectrogram

Key terms

  • time domain
  • frequency domain
  • spectrum, spectrogram, spectral characteristics
  • sinusoid, sine, cosine wave
  • periodic
  • digital
  • discrete
  • sampling
  • sampling rate
  • sampling period
  • Hertz (Hz)
  • bit rate
  • quantization
  • Nyquist Frequency
  • aliasing
  • Discrete Fourier Transform
  • orthogonal basis
  • magnitude spectrum
  • phase spectrum
  • analysis frequencies
  • spectral leakage
  • short-term analysis
  • window function, tapered window
  • window size

› Forums › Courses › Speech Processing › Module 3 – Digital Speech Signals › Signal processing

Viewing 15 topics - 1 through 15 (of 48 total)
1 2 3 4
Viewing 15 topics - 1 through 15 (of 48 total)
1 2 3 4
  • You must be logged in to create new topics.