This video just has a plain transcript, not time-aligned to the videoIn many spoken language applications, we use text data.
That might be the input to a Text-to-Speech synthesiser.
It could be the transcript of the training data for an Automatic Speech Recognise er.
In both cases, we need the text to be made only of words.
One reason for that is because we might eventually need to find the pronunciations, and that might involve looking in the dictionary.
In this video, we're only going to define the problems of tokenisation and normalisation, but not give any solutions.
Those are in other videos and in readings.
Rather, I'll be asking you to think, not just about this particular problem, but more generally about the difficulty of each part of the problem and what kind of solutions would be needed.
Some parts are easy, some parts are much harder.
I'm going to use some conventions from Paul Taylor's book on speech synthesis, starting here with writing the text in the Courier font.
So here is the written form of a sentence.
It is important to understand, this is just a sequence of characters.
These are not yet words.
For example, there's use of case: there's a capital 'H' there.
There are numbers, there's a currency symbol, and there's some punctuation.
To say this sentence out loud, we need to find the underlying words.
We're going to write those in ALL CAPS.
These are all things that we might be able to find in a dictionary.
That's a reasonably straightforward sentence.
But how about this one?
Look how different the written form can be from the underlying words that we need to say out loud.
So how hard can that be?
Well, try it for yourself.
There several parts of this sentence that are not standard words.
What I mean by that is you would not find them in a dictionary.
Can you find them?
Pause the video.
I found this, which needs to be expanded into the word 'Doctor', this, which needs to be expanded into 'the seventeenth' and this, which needs to be expanded in to 'seventeen seventy three'.
My examples are all restricted to English because that's the language we have in common.
But the same problems and the general form of solutions are common across many languages.
Let's start right at the beginning of the pipeline with an apparently easy task: splitting the input into individual sentences.
Why do we need to do that at all?
That's because almost all spoken language technology, including speech synthesisers, can only deal with individual sentences.
In other words, the way they generate speech only uses information within the current sentence.
Can you segment this text into sentences?
Of course, as speaker of the language, you can.
You'll realise that there are just three possible characters that can end a sentence in English: these ones.
From that, you could imagine writing a simple rule that detects these three characters and segments a text into sentences.
Will that work all the time?
Unfortunately not!
There are cases where, for example, a period does not mean the end of sentence.
So even this apparently simple task - of splitting text into sentences - is not entirely trivial.
So have a think about what kind of technique you might need to resolve this problem.
This period is ambiguous.
It could be the end of a sentence, or not.
We need to resolve that ambiguity.
Have a think about whether that's something that you could write down as a speaker of the language.
Maybe you could express it in a rule?
Or would you need to see lots and lots of examples of periods and label them as either 'end of sentence' or 'not end of sentence' and learn something from those labelled examples?
Remember, we're not specifying solutions here.
We're trying to survey the problems and get an idea of how hard they are, and what kind of techniques we're going to need.
In later topics and readings we'll actually provide some solutions.
They might be as simple as handwritten rules that capture the knowledge of a speaker of the language.
Or they might be something more complicated, such as a model learned from data that's been labelled by speakers of the language.
Now that we have individual sentences such as this rather splendid one here, we need to break it down into some smaller units for further processing.
This is still not made of words.
Our goal is to find the underlying words.
So can we just split on white space?
Would that be good enough?
Well, no, not here, because that would leave these as potential tokens.
That's not a word: that expands into 'three inches'.
So once again, have a think about whether you could write down, from your knowledge of the language, a way of tokenising this text reliably.
Or, again, would you actually need to label a large set of data with how it is tokenised and then learn something from that labelled data?
Once we've tokenised (we've broken the text into first sentences, and then the sentences into tokens, which might be words or might not be words yet), we need to decide whether there's further processing required for each of those tokens.
Consider some of the tokens in this sentence.
What do we need to do to expand these into words?
We need to classify them.
We need to decide whether they're already natural language, such as all the things I've just greyed out, or whether they are some other type, such as 'year'.
We then need to resolve ambiguity.
We've detected that this is not a standard word but it's ambiguous as to whether expands into 'Doctor' or 'Drive'.
Once we've detected and classified these types and resolved that ambiguity, we need to verbalise.
We need to turn all these non-natural language tokens into natural language: into words.
So which steps of that do you think are hard and which are easy?
Specifically, consider this token here.
Is it easy to decide whether this should be read as a year 'seventeen seventy three', or a cardinal number 'one thousand seven hundred and seventy three', or as a sequence of digits 'one seven seven three'?
Then, once you've done that correctly - you have decided it is a year - how hard is it to expand that into the underlying words?
There are different steps to the problem.
Some are hard, and some are easy.
One reason that we carefully distinguished written form from the underlying words is that the written form very often contains ambiguity.
We already saw that in the abbreviation 'Dr.', which might or might not have a period after it.
But it's not just abbreviations.
The natural language tokens can also be ambiguous.
When the same written form can denote several different underlying words, we say that it's a 'homograph'.
'Homo' means 'the same' and 'graph' means 'written'.
These are the three ways in which homographs come about.
There are abbreviations, which typically omit characters, which makes words that were distinct have the same written form:
Drive / Doctor.
Street / Saint.
metres / miles.
There are pure accidents such as 'polish' and 'polish'.
I'm going to leave the others for you to think about yourself.
Finally, there are written forms that could denote one of several related underlying words, such as 'record' and 'record'.
All of this ambiguity will need to be resolved before we can determine the underlying words to say them out loud in our Text-to-Speech synthesiser.
But can you do that right now?
Looking at these written forms, could you tell me unambiguously what the spoken word will be?
Of course not!
You need more information.
So the interesting question is, "What information do you need to resolve this ambiguity?"
Let's summarise the key steps in tokenisation and normalisation of text, ready for Text-to-Speech synthesis.
We tokenise the input character sequence into sentences and then into tokens.
Then, for each token, we're going to classify it as either already being natural language or being what's called a Non-Standard Word, which we write as NSW.
That might be an abbreviation, a cardinal number, year, a date, a money expression, and so on.
For both natural language tokens and non-standard word tokens, we need to resolve ambiguity and find the underlying form.
Once we've done that, we need to verbalise the Non-Standard Words into natural language; for example, turning sequences like this into 'seventeen seventy three'.
I've outlined the key problems in turning text - the written form - into a sequence of words to be spoken out loud.
But I didn't offer any solutions, because I want you to think about which parts of this problem are relatively easy and could be solved simply using knowledge from the head of a native speaker encapsulated, perhaps, in rules, and which problems are much harder and can't be solved in that way.
In other words, I asked you think about what types of solution are going to be needed.
These fall into those two broad categories.
In one, it's about linguistic knowledge that could be expressed in a way that can be implemented in software.
In the other, it's not about expressing knowledge directly (for example, in rules), but just using it to provide examples - and we'll call that 'data' - and then learning a solution from those examples.
Both categories of solution have their place in Text-to-Speech and in all sorts of other natural language processing applications.
Let's see where we're going next.
Because we're right at the start of text processing, I'm going to look quite far into the future to try and give you the big picture.
We'll make a first attempt to capture linguistic knowledge in simple rules.
I'll call them 'handwritten' because we're going to go directly from knowledge in the mind of a user of the language to rules that we can implement in software.
We'll see that has some uses, but is limited.
We'll look at then a more powerful and general way to express that knowledge called 'finite state transducers', which we could also write by hand.
With those methods understood, we'll attempt to use them for the problem of predicting pronunciation from spelling.
That can work quite well for some languages.
We can write a pretty comprehensive set of rules for Spanish to do a good job of predicting pronunciation from spelling.
But it doesn't work very well for English.
Have a think about why.
We will then have encountered a problem - predicting pronunciation from spelling for English - that needs more than handwritten rules.
It requires learning from examples: from data.
So, for pronunciation, and for other problems such as predicting prosody, we need some way of learning from data.
We meet machine learning for the first time, and we going to look at decision trees.

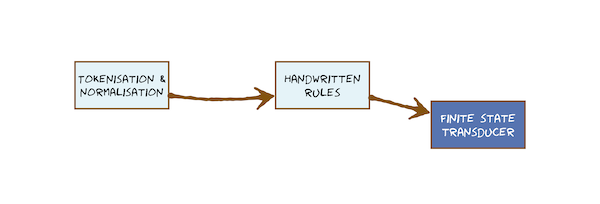
This video just has a plain transcript, not time-aligned to the videoThe first stage in Text-to-Speech is to tokenise the written form and normalise it into a sequence of words.
We've already seen that that's non-trivial because the relationship between written form and underlying words can contain a lot of ambiguity.
That means we now need to develop some techniques for performing tokenisation and normalisation, and some subsequent tasks that are coming up, such as determining pronunciation.
I've already asked you to think quite a lot about the methods that you might use.
I've given you some strong hints that sometimes the best solution involves using your own linguistic knowledge, or the linguistic knowledge in the mind of a native speaker of the language, and capturing that in a form that can be implemented in software.
An obvious form to capture that knowledge would be as rules.
I'm going to call them here 'handwritten rules' to distinguish them from other rules and rule-like systems that might be learned from data that we'll encounter further on.
Let's try tokenising a sentence by rule.
I've written it here in a programming language: in Python.
Don't worry if you don't know Python; you should still be able to read this code.
We've got some input and we're just going to scan through the characters.
If the input character is a white space, we'll split.
In other words, there's just one rule, and the rule is here.
If the character is equal to white space, we split.
Now that's such a simple rule, there's no problem implementing it in this little fragment of software.
That works fine for this really simple rule.
But it's actually very bad engineering practice, because there's no separation between where the rules are and the general engine that applies the rules.
The rules are deep inside the code here.
The engine that applies them is the thing that scans through the characters and applies the rule character by character.
If we decide this rule is not quite good enough - we want to change it - we have to change code.
It would be much better to have some separation between the code and the rules.
There are lots of different formalisms for writing rules.
We're not going to get too hung up on the fine details of them, but here's one.
They're called context-sensitive rewrite rules.
I'm not using any particular notation for writing these.
Hopefully it's intuitive and easy to understand.
The rules are here, and they say that if you've got this token, then it rewrites to the following characters if you find it in the context of a capitalised word to the left and anything at all to the right.
So these rules mean if you find these characters after a capitalised word, it should be 'Drive' and if you find it before a capitalised word it should be 'Doctor'.
The big advantage of rules is that they're human-friendly.
We can write them down by hand and other humans can read them and understand them.
But there is a downside, and one downside is that they're going to be sensitive to the order in which you apply them.
In particular, if we come across a case where 'Dr.' is after a capitalised word and before a capitalised word, the order of application of the rules will change the result.
Now that might be a rare case, but still it's a bad property of rules.
So these are just rules, and we would have some general-purpose software that applies them.
If we wanted to, we could update them at any time, or swap them out for a set for another language, without changing the software - the code - at all.
That's good engineering.
Context-sensitive rewrite rules examine the immediate context, but sometimes we might need to look across the entire sentence.
Here are some rules of a similar form that do that.
This rule says that, if you find this spelling, you should annotate it as being a fish if any of these other words occur in the same sentence.
But if you find any of these words in the same sentence, you should annotate as the musical term.
I'm not claiming these are comprehensive rules or even very good rules.
Again, don't get too hung up on the way of writing the rule down.
I'm not using any particular notation.
Just understand the general concept that there are some things we could write down rules for, if we think we can come up with a comprehensive set of rules and, in this case, a comprehensive set of these trigger words that tell us how to disambiguate 'bass'.
For some problems in spoken language processing, handwritten rules are the right thing to do because they have some nice properties.
They directly capture linguistic knowledge from a native speaker, and that's acquired over a lifetime of experience.
That speaker has distilled all of their data that they've been exposed to - all the language they've experienced - into some internal representation, which we ask them to express directly as a rule.
So we're effectively using a very large amount of data there, without having to go and gather that data directly.
They're going to be computational efficient, they are very small to store, and very fast to apply.
They're interpretable, so we can write them down and then come back to them later and still understand them, and modify them, and improve them.
That's not going to be true for many forms of machine learning.
Context-sensitive rewrite rules and collocation rules are one option.
But there is a more general formal framework in which you can write down something that looks like rules, and that's called a 'finite state transducer'.
That's a very important class of model because it could be created by hand, either directly or by compiling a finite state transducer from some other formalism, such as a set of rules.
Or, importantly, it could be learned automatically from data.
So next we could look a finite state transducers for performing some text processing tasks in speech synthesis.
But much later on, we'll come back to finite state models again when we do Automatic Speech Recognition.
Whilst rules are sometimes the right answer, they're not always.
In the case of rules, we can very quickly end up with large sets of rules with complicated interactions, so their output is sensitive to the order in which we apply them, and then they become much harder to maintain.
Rules are just one tool in our toolbox.
For some languages, handwritten rules are sufficient for determining the pronunciation of words.
Unfortunately, English is not one of those languages, and so that's a case where we're going to need to use a model that can be learned from data.
For that we'll choose a decision tree.

This video just has a plain transcript, not time-aligned to the videoWhilst rules can work well in some simple cases, sometimes we need a more powerful technique.
One possibility is a finite state transducer.
We'll look at them here as a generalisation of handwritten rules, and that means we're just going to be creating a finite state transducer by hand, for now.
Remember that the input to our Text-to-Speech system is just a string of characters.
There are no words; we have to find them.
To find the words we need to tokenise, classify, resolve ambiguity, and verbalise.
This video is about finite state transducers, which could be used to classify non-standard words as well as to verbalise them.
Let's use the two non-standard words in this sentence as examples and just focus on the process of verbalization.
That means we've already detected that this is a year and that this is a money amount.
Some parts of verbalization might be non-trivial.
The pound symbol is at the beginning of the written form, but the end of the spoken form.
So we need some machinery that can deal with that.
Now, this is not a complete course on finite state transducers.
That would be part of a larger topic of formal languages in either computer science or computational linguistics.
Here we're just interested in their capabilities.
Capturing our own linguistic knowledge and expertise is a perfectly valid approach to solving some problems in Text-to-Speech and spoken language processing more generally.
One challenge in doing that is to find a suitable form in which we can express our knowledge.
Rules are one option, and they will often need to access the context of the token we're processing.
We saw context-sensitive rewrite rules and collocation rules doing that.
Finite state transducers are another option.
They're closely related and, for our purposes, let's just say they're part of the same family of approaches.
Here is a simple finite state transducer.
It's made of states and there are, of course, a finite number of them.
The notation I'm using is that there's a start state, and that's bold.
There's an end state written with two circles.
Then normal states written like that.
Those states are connected by arcs, and it's on the arcs where the action happens.
The action involves the finite state transducer consuming some input and emitting some output.
The arcs are directed: they have arrows on them.
Let's make everything clearer with a concrete example of verbalising the numbers 10 to 19.
I'll have a start state and then we'll go to the next state and we'll consume the first digit '1'.
But we can't emit anything yet because we don't know whether it's going to be 10 or 11 or 17 or 19.
So we write 'epsilon' for emitting nothing.
This state has meaning.
The model has no external memory, no place to store anything; it only has states and arcs.
This state means we have consumed '1' and we're waiting to see what happens next.
So, in fact, the states are the memory of the network.
The more we have to memorise before we can emit anything, the bigger this network is going to have to be.
All we can do next is consume another character.
We consume a '0' and now we can emit the word 'ten'.
Consume a '1' and emit 'eleven'.
Given any of those individual numbers 10, 11, 12, up to 19, this machine will consume the input and emit a word as output and then finish in its end state.
This transducer only handles 10 to 19.
So, on your own as an exercise, try expanding it (just with pencil and paper) to verbalise all numbers from 10 to 99.
You should make the network a small as possible.
In other words, with as few states as possible.
Let's do another example, this time years such as this one here, which we read as 'seventeen ninety'
We consume the digits one by one and optionally emit some output.
We can consume the '1' but we can't say anything yet.
We can consume the next digit, and now we can say 'ten', 'eleven',...'seventeen',...
In this case, we'd have consumed the '1', consumed the '7', and emitted 'seventeen'.
Then we consume the next digit, and we can say, for example if it's a '9' we've just consumed, we could immediately emit 'ninety'.
We don't need to wait for any more input.
Then the final digit: if it's a '0', we emit nothing, otherwise, we emit 'one' to 'nine'.
This finite state transducer once again works for some years, but not all.
First of all, I want you to, as an exercise on your own, decide which years it will work for and which it won't.
Then improve it handle all possible four digit years.
Let's set a reasonable range on that: let's go from 1066 to 1999.
If you succeed in doing that, then extend it into the 21st century as well.
A final example: money amounts in which the currency symbol is written at the start but spoken at the end.
Have a go on your own.
Pause the video.
Well, hopefully you have understood that the model needs to memorise things by having states.
So this model needs a start state and an end state, as they always do.
We need to consume the '£' symbol, but we can't emit anything yet.
This state means that we've seen a '£' symbol and we're waiting to see what happens next.
Towards the end of the finite state transducer, we'll have to emit the word 'pounds'.
Let's write an arc for that.
There won't be anything to consume.
We've already consumed the '£' symbol.
Somewhere in the middle you need a finite state transducer that is a general number expander.
I'll let you have a go writing one.
If you manage that, try generalising to multiple currencies in which the symbol is written at the beginning but the word is said at the end.
I'll give you a hint on how to do that.
It can use the same number-expanding finite state transducer, but it'll have to do something different at the beginning in the end.
Then you'll have discovered a really useful property of finite-state transducers: that we can join together smaller ones to make larger ones.
Here, we reused a general purpose number expander, to expand currency amounts.
That's good engineering.
We build one good number expander, and then use it many times.
This is the end of this little sequence of topics on text processing.
But finite state methods are really important, and they're going to reappear much later, in Automatic Speech Recognition.
They could be used to model language: in other words, the possible sequences of words, and perhaps their probabilities of occurring.
They can also be used as the basis for a model of speech itself.
If we have a model of language (of word sequences) and a model of speech, we can then take advantage of this ability to combine small, finite state models into larger ones to make models of complete utterances from models of smaller things such as words or sub-word units like phonemes.

This video just has a plain transcript, not time-aligned to the videoTo convert text into speech, we first have to find the words by tokenising and normalising the input text.
The next step is to determine the pronunciation of each word.
We've seen that speech sounds form categories.
They're called phonemes, although we haven't carefully defined that term yet.
We're going to use those to specify the pronunciation of words.
Some steps in tokenisation and normalisation were performed with handwritten rules.
We could imagine, at least for now, using the same approach for pronunciation.
We would write rules that map the spelling of the word - which is a sequence of characters - to its pronunciation - which is a sequence of phonemes.
That's going to work for some languages, but not all.
Here's the IPA vowel chart again.
There are a lot of possible vowel because of every possible combination of height (4 values in this chart), advancement or front-back (3 values), and rounding (2 values).
That's 4 x 3 x 2 = 24, and then there's a few in-between ones to give us even more.
No language in the world uses that many vowels.
But why not?
The reason is that nature is very good at finding efficient solutions, and using all of those vowels would be very inefficient.
If speakers had to make that many vowels, they would have to be extremely precise with their articulator positions, and that would take a lot of energy.
Listeners would also have to expend a lot of effort in perceiving these very small differences.
So, when I say nature is very good at finding efficient solutions, I mean ones where we can be lazy and expend as little energy as possible.
So languages tend to have far fewer vowels than this.
A lot of languages have settled on having 5 five vowels as a good number, for example, like Spanish and Japanese and many, many more.
Whatever vowels a language uses, they're going to be widely dispersed around the vowel space to make it easy to produce and easy to perceive.
No language in the world would pick these four vowels, for example.
If a language has evolved to have 4 vowels, they're quite likely to be in the corners: to be far apart, acoustically and perceptually.
Vowel space is acoustically continuous.
There are no boundaries.
There are no categories.
We can make any combination of the two formants that we like.
So, of all the available vowels in the IPA chart, how do we discover which ones a particular language uses?
In other words, where in this continuous vowel space might we draw some category boundaries between the different vowels?
To put that another way: how do we tell the difference between variation within categories (which a speaker is going to make because they're not being precise, but which a listener will hear as the same category), and variation that crosses a category boundary?
Here's how you do it, if you were documenting a language for the first time.
With the help of a native speaker, you'd look for pairs of words (or at least, possible words) that differ in only one sound.
If a single sound change makes the word change, than that pair of words is called a 'minimal pair' and the two contrasting sounds are different phonemes in that language.
That's the definition of a phoneme.
You'll see that I'm now writing the phonemes inside slashes like this.
Earlier, I had them in square brackets.
The slashes mean that this is a string of phonemes - of abstract categories.
There's no speech signal here.
The square brackets used earlier indicated that I was transcribing actual speech.
These are some minimal pairs that tell us about vowels in English.
'bit' and 'bet are different words, so /ɪ/ and /e/ are different phonemes.
'bit' and 'beat' are different words, so /ɪ/ and /iː/ are different phonemes.
That doesn't just work for vowels; that works forconsonants too.
'bit' and 'pit' are different words, so /b/ and /p/ are different phonemes.
Now, you'd be excused for thinking that the phoneme inventory is going to be very well-defined for all the languages we might ever want to build a Text-To-Speech or Automatic Speech Recognition system for.
Unfortunately not!
The phoneme inventory is an internal part of the system: it's not exposed to the users.
So it's available to us as one of the many design choices that we'll need to make as the system designers and builders.
To give you an idea of that sort of choice, let's consider allophones.
Sometimes there are two sounds which we think might be different phonemes because they're acoustically different, but we just can't find any minimal pairs in the language.
Here are some English words containing /l/ sounds.
The word-initial one is often called 'light l' and word-final one is often called 'dark l'.
They're produced with slightly different articulator positions and they have slightly different acoustics.
But you'll never find a minimal pair that differentiates between dark l and light l - they're called allophones.
Dark l and light l are just one example of allophonic variation.
Now, since we are the system designers it is up to us whether we want to use the same category for both dark and light l, or have them in two categories.
For Text-To-Speech, where we are generating speech and we want the acoustics to be right, and the acoustics be different for each of these dark and light ls, we'll probably want different categories - in other words, different symbols.
But for Automatic Speech Recognition, since the difference never distinguishes two words, then perhaps using the same category (the same symbol) would be fine.
So for Automatic Speech Recognition, we might have the pronunciation like this for this orthographic word.
But for speech synthesis, we might have it like this and use a different symbol for the dark l.
This isn't a complete course on phonology, which is that part of linguistics concerned with categories of sounds.
You need to take a course on that alongside these videos.
This video is really just to make the connection for you between sound categories and our two applications of Text-To-Speech and Automatic Speech Recognition.
So, let's continue with that.
Now we have a much clearer definition of what a phoneme is, we can get back to the problem we're currently trying to solve: converting a string of characters into a string of phonemes.
This is commonly called grapheme-to-phoneme conversion, although the input is characters, so "G2P", but you'll also find it called 'letter-to-sound'.
Here I've attempted to write down some context-sensitive rewrite rules for G2P.
On the left for Spanish, and on the right for English.
Like in the Handwritten Rules video, I'm not using any particular formalism for formatting these.
There are many ways of doing it, and in fact this notation is different to the previous videos.
We're not going to get hung up on notation!
This rule says that the character 'a' goes to the phoneme /a/ regardless of the context it occurs in.
This rule says that the character 'c', when it's going to be followed by the character 'i' goes to the phoneme /θ/.
Already, you can see that the rules for Spanish look nice and simple, and the rules for English are already considerably more complicated.
In fact, for Spanish, around 50 rules will cover everything.
Those can be written by hand and work well.
That's just not possible for English, because there are so many exceptions.
Try it for yourself if you want to try and prove me wrong!
For English, and some other languages, the only reliable source of word pronunciations is a dictionary: a large table of orthographic forms and their pronunciations, written by an expert lexicographer.
But even the largest dictionary can never cover all the words in the language because new words are invented every day.
What we need to do is to have a large dictionary and extrapolate from that to all the new words that aren't in the dictionary.
We need a way to learn from all the examples in the dictionary and automatically create G2P rules.
We'll treat the dictionary as data and we'll use machine learning to create our set of rules.
Now the 'rules' may or may not actually be rules.
So in general we should stop saying 'G2P rules' and start talking about a 'G2P model'.
We won't throw our dictionary away.
When performing Text-to-Speech, we'll always look for a word in the dictionary first, because it's reliable, and only if it's not there resort to G2P.
Exactly what our dictionary contains might vary depending on our application.
The first line on this slide is a transcription written in the IPA.
It's written in square brackets to indicate that.
In other words, that's the transcription of how somebody actually said this word.
That's actually not a dictionary entry.
The second line is a dictionary entry that might be used for Automatic Speech Recognition.
The symbols are not in the IPA, but that's just a convenience to make them machine readable.
That difference isn't important.
The difference that is interesting is between the Automatic Speech Recognition dictionary and the Text-to-Speech dictionary.
This one is for ASR.
This one is for TTS.
This 3rd line is much richer than the others.
It has extra information.
It shows syllable structure.
Fro each syllable, it indicates - with the number 1 or some other numbers - which syllables have lexical stress.
So this word is said 'impossible' with stress on the 2nd syllable; that's marked with this '1' here.
The TTS dictionary writes all the vowels as their full vowels.
It doesn't write anything as /ə/.
So it will be the job of the TTS system to decide whether the vowels in some of the unstressed syllables reduce to /ə/ as they were in this transcribed speech.
This symbol is a syllabic /l/ : that indicates a consonant that can form a syllable without needing a vowel.
Finally, the TTS dictionary might include Part-Of-Speech (POS) information, because that helps us look up the correct entry in the case of homographs.
The key point to understand here is that the dictionary (and its phoneme set) is something where there are design choices to be made, and that we might make different choices for different applications.
We've defined the phoneme and we're going to use it to write down pronunciations of words, either by writing a dictionary or by learning from that dictionary a G2P model.
What we need now, then, is some machine learning to solve that problem of G2P.
Machine learning can offer us all sorts of different types of models that we might choose from.
We're going to start with something very simple, but that actually has a very wide range of application.
Decision Trees can be used in lots and lots of problems where we make predictions about something.
That 'something' can be symbolic or numerical.
Those predictions are based on knowing the values of some predictors.
Those can also be of any type we like: symbolic, or numerical.

This video just has a plain transcript, not time-aligned to the videoThe same written sentence can be spoken in many different ways.
Perhaps the most obvious thing a speaker can vary is the F0 contour, which is perceived by the listener as variations in pitch.
The speaker can also create variations in amplitude and duration.
The speaker is varying the prosody of the utterance.
Prosody is an area of linguistics where there are too many competing theories on lots of disagreement.
But don't worry!
We're going to avoid all of that and keep things as simple as possible.
Here's a text sentence and a possible pronunciation written using the IPA.
This already tells us a lot about how to say this text out loud.
For example, it's already told us which vowels were going to get reduced to /ə/, compared to the dictionary entry for this word.
But this pronunciation doesn't specify everything we need to know before saying the sentence out loud.
If we want to create natural-sounding synthetic speech, we need more than this.
We're going to have to predict the fundamental frequency contour, the duration of each phoneme and, for longer sentences, perhaps where to insert pauses.
So again, without getting into any particular theory of prosody, here's a working summary that will be good enough for our purposes.
On the left are the linguistic functions that prosody performs in communication.
Phrasing is about how the words in a sentence form groups that are smaller than the sentence.
Rhythm is about timing and speaking rate.
Emphasis is about speakers placing relative importance on some words in a sentence, compared to others.
Intonation is the use of pitch - for example, to indicate a question.
There are also some paralinguistic functions ('para' means 'alongside') and those involve generally knowing more than just the text, so we're not going to cover them in this course.
On the right are the acoustic correlates: the things that happen to the speech signal.
Since all we're doing is synthesising speech - we're making speech signals - all we really need to do is predict those acoustic values.
Now, voice quality cannot easily be controlled in most systems, so let's forget that one and focus on the job of predicting F0 and duration.
We're going to do that step-by-step.
Before predicting the duration of phonemes and the fundamental frequency contour, we need to predict how our sentence breaks into prosodic phrases, which might be marked by pauses or by movements in F0.
We could consider this task to be part of text processing because we'll need to use text features to do it: that's all we have available.
Often, punctuation is a good indicator.
Commas often indicate places where the speaker could (or should) break the sentence into phrases.
A comma could be marked with a pause, but it's not the only way.
You can use movements in F0 and changes in duration as well.
But using only punctuation is not good enough.
Listen to a speaker reading this sentence.
"Presently Wilbur raised his head and began speaking in that strange, resonant fashion which hinted at sound-producing organs unlike the run of mankind's."
I can hear clear phrase breaks after 'presently' and after 'fashion'.
There's no punctuation there.
In fact, the only comma in this sentence is part of a list structure and the speaker didn't make a phrase break there.
So this problem is not as trivial as just finding the punctuation.
After predicting where to break the sentence into phrases, we might predict the duration of each segment: of each phoneme.
The duration of a phoneme depends partly on its identity.
For example, /m/ is intrinsically longer than /p/.
Duration also depends on the context in which this phoneme is being spoken.
We therefore need to predict the duration of each of these using information about its identity and the context in which it occurs.
That context could be the neighbouring phonemes or anything else we have available, such as where it is within a syllable, whether that syllable has lexical stress,...
Then, having predicted duration, we need to place an F0 contour on the utterance.
Although we're not subscribing to any particular theory of prosody, we can say that most linguists would agree that the syllable is the smallest meaningful unit when it comes to F0 variations.
So we will make predictions on a per-syllable basis, not per-phoneme.
Here's a naturally-spoken sentence.
'Nothing's impossible.'
To understand the problem of F0 prediction, let's see how close we could get to that natural sentence with some very simple F0 contours.
Start with the simplest one of all: a constant value, monotonic F0.
'Nothing's impossible.'
OK, not very natural at all!
Speakers tend to gradually decrease F0 over the course of an utterance.
That's called 'declination'.
'Nothing's impossible.'
Well, that already sounds a lot better.
Clearly not natural, but much better than before.
Another thing speakers do is to place some F0 movement on some of the syllables in some of the words.
So I'll choose one syllable from each of the two words in the sentence: the one with primary lexical stress.
This one and this one.
I have chosen where to place intonation events and I'm going to now choose what type of event to use: what kind of movement F0 will make.
I'll use the simplest one of all, which is a simple rise and then fall of F0.
So I'll just put some little bumps on those two syllables.
That sounds like this.
'Nothing's impossible.'
And that's not bad for such a very simple F0 contour.
Let's just hear the natural one one more time.
'Nothing's impossible.'
OK, so we got somewhere close to the natural one with this very, very simple F0 contour: a declining baseline with a couple of rise-fall accents.
Now, this point, if this was a whole course on prosody, we would have to have a long argument about what types of intonation events exist (rises, falls, rise-falls,...), how many types there are, and so on, and so forth.
But don't worry, we're not going to bother ourselves with that argument!
I talked about prosody and I reduced the problem to one of predicting things in a particular order.
Predicting phrase breaks, then phoneme durations, and then F0, which we reduced to predicting which syllables receive some event and then what sort of event that is.
But I actually didn't provide any methods for making those predictions.
That's because all of these tasks are now too hard for handwritten rules.
As with predicting pronunciation from spelling (for English, at least), we need something more powerful than rules.
We need machine learning.
All the problems I've just outlined in this video are all going to be solved with machine learning.
They're all problems in which we predict something, given some other information: some contextual information.
We're going to predict prosody and pronunciation using machine learning.
Our first encounter with machine learning will be a decision tree.
Unlike most forms of machine learning, decision trees are - to some extent - human-friendly.
That means we'll be able to inspect the model that has been learned from data and understand how it works.
We could even attempt to write a decision tree by hand.
But to be clear, this human-friendliness is just a bonus.
It's not our top priority in machine learning.
It's just 'nice to have' sometimes.

This video just has a plain transcript, not time-aligned to the videoWe've already found a need to make predictions.
We might encounter a word that is not in our dictionary and therefore need to predict its pronunciation from its spelling.
Or we might need to predict the duration of a phoneme, given its linguistic context.
Or predict where to place intonation events, and from those predict values for F0, as part of prosody prediction.
All of these tasks have one thing in common.
We know the values of certain properties already and from those we want to predict the value of one further property.
Those properties can be anything.
They could be discrete categories or continuous values.
So we need a general-purpose method that can make predictions in this situation.
A Decision Tree is one such general-purpose method.
I've been trying to write some G2P rules for English.
I'm using my own knowledge of the language to do that.
Here are some rules that I've come up with for the letter 'c'.
The rules read like this.
That's the letter I'm trying to predict the pronunciation of.
That's the previous letter.
That's the next letter.
This underscore means there wasn't a previous letter; in other words it's word-initial.
This isn't a complete set of rules by any means, but it's good enough for this example.
I know the spelling and I'm predicting the pronunciation.
Let's introduce some terminology to talk about that.
Since I believe spelling can be used to predict the pronunciation, the letters are called 'predictors'.
The thing I'm predicting is the 'predictee'.
There are several predictors, so let's give them names: 'C' for the current letter; 'P' for the previous letter; 'N' for the next letter.
Rules are a valid formalism, but it can be difficult to cover all possible cases.
For example, my rules don't yet tell me what I need to do for the case: the letter 'c' preceded by 'i' and followed by 'o'.
They simply don't tell me.
So let's change formalism to one that always covers all cases: a Decision Tree.
To introduce the Decision Tree as a concept, I'm going to use these rules as the starting point, but that's just to help you see the relationship between a list of rules and a Decision Tree.
Later, we'll see that a Decision Tree is much better learned directly from data.
In my little set of rules, the letter 'c' is pronounced as one of 4 possible phonemes.
'Which one?' is the thing we're trying to predict: the predictee.
In this formalism of a Decision Tree, we're going to ask questions about things we know: the predictors.
We're going to gradually narrow down the possible values of the predictee.
We're going to limit those questions to be simple 'yes or no' questions (or 'true / false' if you prefer).
For example, let's query the next letter as the predictor.
If the next letter is 'h', we'll predict that the possible phonemes have been narrowed down to just 2 of the 4.
We're now more certain about how to pronounce the letter 'c'.
Otherwise, it'll be one of the other phonemes.
We're still not certain of the exact phoneme but we've narrowed the possibilities down.
We've reduced our uncertainty.
We can carry on.
Try asking another question.
Let's try distinguishing /ʃ/ from /tʃ/.
This question asks whether we're at the beginning of a word.
If we are, the 'c' is pronounced as /tʃ/.
Otherwise, it's pronounced as /ʃ/.
We could also try to distinguish /k/ from /s/ with another question.
How about asking whether there's an 'o' after the 'c'?
If there is, it'll be pronounced as /k/, otherwise /s/.
This tree is complete and it will make predictions for all possible cases, even ones that were not in the rules.
That's because the answer to every question is either 'yes' or 'no'!
Between them, 'yes' and 'no' cover all possible cases.
This is then a complete Decision Tree.
We can use it to make predictions for any case.
So let's try it.
How do you pronounce the letter 'c' in the word 'coffee'?
Well, just follow the Decision Tree.
Start at the root.
Is there an 'h' after the 'c'?
No, there isn't.
Is there an 'o' after the 'c'?
Yes, there is.
It's pronounced as /k/.
Let's try another word.
Start at the root of the tree.
Is there an 'h' as the next letter?
No.
Is the next 'o'?
No.
We reach a leaf and we predict that the pronunciation is /s/ : 'cyan'.
Try it for yourself.
Find some words containing the letter 'c' and see how often this tree makes the correct prediction.
Pause the video.
I hope you found lots of words where the tree makes the correct prediction.
The tree's not perfect.
It gets it right some of the time, but not all of the time.
This is just a handwritten Decision Tree.
It covers all possible cases.
It covers cases that our rules did not.
So it's already much better than those rules.
But in fact, the tree is nothing more than rules, arranged now into a tree structure rather than in a list.
In other words, the answer to one question determines which question we ask next.
It might be different along the two branches.
Decision Trees have many attractive properties.
We can, if we want, create them by hand, and that's what I just did.
But that's actually not the normal thing to do.
We're going to see in the next topic that we can learn them automatically from data.
In other words, we can employ machine learning to obtain a tree from a set of data points.
Decision Trees are interpretable.
We can draw a picture of them, like this.
That's really nice, and that will still be true even when the tree has been learned automatically from data, because a tree is just a tree
Interpretability is a nice thing to have, and it's not always there in other machine learning methods
Decision Trees are typically compact.
The tree in this picture only has to ask two questions to arrive at a value for the predictee.
If implemented in software, that will be extremely fast.
That will still be true even when the tree becomes much larger (and that will probably happen when we learn one from data), because the number of computations in the tree to do inference - in other words, to make a prediction - is proportional to the number of questions to ask.
That's to do with the depth of the tree, not the width of the tree.
We always draw Decision Trees this way so that decisions flow from top of the page to bottom of the page.
Real trees are this way up.
We're just drawing them upside down.
The type of Decision Tree that we've made is called a 'CART' (Classification And Regression Tree).
Now the tree can either do classification or regression, but not both at the same time.
So 'And' should really be 'Or'.
In a Classification Tree, the predictee is a categorical variable.
It takes on one of a fixed number of possible values, or classes.
In a Regression Tree, the predictee is a continuous value.
Here, I've made up a tree that predicts the height of an F0 event based on the stress level of a syllable.
This tree is doing regression.
Decision Trees, whether they are Classification Trees, or Regression Trees, can be learned from data.
So that's what we'll look at next.
It's time for some machine learning!
But before we do that, let's be very clear that a Decision Tree is a Decision Tree, regardless of whether it was hand-crafted or learned from data.
We won't be able to tell by looking at a tree how it was made.
So we must make a careful distinction between the model (here, the Decision Tree) and the algorithm used to learn that model.
This topic video was about the model and the next topic is about the algorithm.
That's a very important distinction in machine learning, that you must get clear in your mind: a distinction between the model and the algorithm used to learn the model.

This video just has a plain transcript, not time-aligned to the videoLet's start with a reminder.
We need to be very clear that a Decision Tree is the model.
A Decision Tree is a Decision Tree, regardless of whether it was handcrafted or learned from data.
We must always make a careful distinction in machine learning between the model (here, it's the Decision Tree) and the algorithm used to learn that model.
The previous topic introduced the model and now we're going to introduce the algorithm.
As an example we'll use G2P.
This video is going to keep things fairly short and simple.
To really understand Decision Trees, you'll need to do some worked examples.
In my previous attempts to create a G2P model for English, I started from the knowledge in the mind of a native speaker.
In that case, it was myself.
That speaker expressed the knowledge as a set of rules.
We then saw how we could compactly write those rules as a Decision Tree.
The Decision Tree is better than the rules in the sense that it will generalise to any case that wasn't covered by the rules.
But why ask our Native Speaker to write down rules at all?
The rules might not cover all cases.
We might have difficulty in deciding the relative importance of the rules and getting them in the right order.
We're going to move away from rules to a Decision Tree, which is effectively a way to arrange rules (which we'll now call 'questions') whose answer is either 'yes' or 'no' ('true' or 'false') in the best order, with the added advantage of covering all cases.
But instead of going from the mind of a native speaker to rules, and from rules to a tree, let's cut out those rules and work straight from data.
So what would that data be for G2P?
Well, it will be a list of words: spellings and their correct pronunciations.
That's still knowledge distilled from the mind of a native speaker.
So we'll replace imperfect rules with reliable data points.
This data is, in fact, just a pronunciation dictionary.
So now the question is: how to learn a Decision Tree from these data?
To keep my example simple, I'm just going to use words with a single letter 'c' that is is pronounced as 1 of 4 phonemes.
Here's some of my data.
The thing we're predicting (the predictee) is the phoneme that the letter 'c' will be pronounced as.
A predictors, I'm going to choose a window of letters centred around the letter 'c'.
This choice to use a window of letters is another place where knowledge is being incorporated into the model.
This time, it's knowledge from me, the 'Machine Learning Engineer'!
Machine learning isn't just about data and model; it's about all the choices that we have to make along the way.
Now we simply extract from this raw data the predictors and the predictee.
This process - going from raw data to the set of data points that we're going to do machine learning with - involves some decisions.
Here, the decision was to use a window of letters: +/- 2 letters around the letter 'c'.
All the predictors have to have a value all of the time.
That's involved padding in cases where we're at the end or the beginning of a word.
Padding at the start and end of a sequence is often necessary when we use a sliding window, just like in signal processing.
On the right are our data points.
Each of these is an individual data point, of predictors and the correct value for the predictee.
Now we can discard the raw data.
Here's some of my data set.
There's lots and lots more of that.
In fact, from the dictionary I was extracting this data from, I obtained a total of around 16,500 data points.
From those data, we are going to learn a Decision Tree.
I'll call this the 'training data'.
The words 'training' and 'learning' are both used to refer to the procedure for automatically estimating a model from data.
In the case of Decision Trees, the term 'learning' is the usual way to describe this procedure.
Machine learning means learning from data.
What are we trying to achieve?
Well, we're trying to generalise from all of these data points that we've seen before, to a new data point.
Given the letter 'c' in this particular context, we have to make a prediction for the phoneme to pronounce.
A typical machine learning technique, then, is to learn a model from the data in a learning or training phase, and to use that to make the predictions.
From the data, we learn a model.
The model is what we then use to do inference, which is the process of taking the predictors and predicting the predictee in a previously-unseen data point - a new data point.
Sometimes that phase is called the 'testing' phase.
Here, the model is going to be a Decision Tree.
We're talking about learning that Decision Tree from the data.
Back to the training data.
I'm just showing you a sample.
In total, there are 16,500 training data points.
Let's start by considering the probability distribution of the predictee.
It's a phoneme and it takes 1 of 4 possible values.
There's the distribution.
This histogram is the probability distribution over the phoneme value, which is on this axis.
We can think of these bars as the data points.
So think of this bar is made of all of those /k/ data points: this one, this one, this one, this one, and so on.
They're all in that 'bucket' there.
Now, if you had to predict how to pronounce the letter 'c' and I didn't tell you anything more than that, I think it's pretty obvious that you'd predict /k/, because that's the most frequent value in the training data.
You'd be correct a lot of the time (most of the time, in fact).
So we can make a prediction already.
But of course, we know more than that.
We know the values of the predictors: the surrounding letters, +/- 2 letters.
We should make use of that information by asking questions of it: by querying it.
Let's imagine the ideal Decision Tree that we could learn from our data.
This distribution is of the entire training data.
We find a question about the predictors that beautifully splits this data like this.
Some question - to be found - that splits all the /k/ and /s/ into one partition, and all the /ʃ/ and /tʃ/ into the other partition.
If the answer to that question was 'yes', we'd continue to predict /k/, because that's still the most frequent value here.
But if the answer to this question was 'no', we'd predict /tʃ/.
Now we're going to be correct more of the time than just predicting /k/.
Then we continue.
We find other questions that perfectly split these two partitions of the data.
We find a question here that splits this beautifully into all the /k/ and all the /s/.
We find another question over here that beautifully splits that partition into two smaller partitions of /ʃ/ and /tʃ/.
Now we've got a perfect Decision Tree.
This Decision Tree will correctly predict the pronunciation of the letter 'c' as 1 of these 4 phonemes, and it will be 100% correct: it'll be right all of the time, at least for the data points in the training data.
So what has the tree done to the distribution of predictee values?
It's made that distribution more and more certain.
In this perfect tree, at the leaves, we become completely certain that, if we reach this leaf, it's always /tʃ/.
100% of the data points are /tʃ/ and none of the other values occur.
This distribution has zero entropy: there is perfect certainty.
As we partition the data going down the tree, we increased certainty at every level.
In other words, we reduced entropy.
Each question that we asked about the data partitioned it into two partitions.
That reduced the entropy, compared to before the split.
This particular tree might not be possible.
There might simply not be any question that splits the data in that way.
The real tree won't be quite so perfect.
Let's find out!
Back to the training data.
We already said that, if we wanted to make a prediction right away without asking any questions about the predictors, we'll just pick the most common value of the predictee found in the training data.
We can compute that by looking at this distribution and picking the highest bar.
Well, we've already got a Decision Tree.
It's only got a root node.
The root note says 'Don't bother asking any questions! Just predict /k/.'
In my training data set, that will be correct about 68% of the time, for the training data.
That's not bad, for not asking any questions, but we can do better.
We'll put that at the root of a tree.
We're now going to try partitioning this training data into two partitions that have lower entropy than this distribution here.
The questions, of course, have to be about the predictors: about the letters.
We have 4 predictors and each of them can take on values of the 26 letters or the underscore, or 27 possible values.
4 x 27 = 108.
So there are 108 possible questions we could ask.
Let's try one.
Let's ask 'Is the next letter 'e' ?'
If it is, some of the data goes this way.
We could look at the distribution of that data: it looks like this.
We predict /s/ as the pronunciation with quite a lot of certainty.
If the next letter isn't 'e', all the rest of the data goes this way.
We can look at its distribution and we'll continue to pronounce this letter 'c' as /k/.
Just visually, we can see that this distribution obviously has fairly low entropy: it's dominated by a single value.
This one has a little bit lower entropy than all of the training data.
So the total entropy in these two partitions is lower than the entropy in the original data.
But that was just one possible question.
We need to try all of the other 107 questions available to us.
Back up to the root, where we're predicting /k/ all the time.
I did try all 108 questions for this data (which is real data) and I found that this question 'Is the next letter 'h' ?' was the one that gave the best split.
It reduced entropy by more than any other question.
So I put it permanently into my tree.
I'm now permanently partitioning the training data into these two partitions.
The most common value on the left is /tʃ/ and the most common value on the right is /k/.
This is a complete Decision Tree, and we could stop here or we could continue.
To continue, we simply take this and recurse with the same procedure.
We take this as the training data.
We try partitioning with every possible question and seeing which question can further reduce the entropy.
Then we do the same on the right node.
Here's what actually happens for this real data set.
I'm just going to now show the best question in each case.
That was found by trying all of the possible ones and measuring the entropy reduction.
I split this left node by the question 'Is the previous letter 's' ?'
That split the data like this.
I labelled the leaves with /ʃ/ and /tʃ/
On the right, I asked the question 'Is the next letter 'e' ?'
That was the best one, chosen out of all the possible questions I could've asked.
If it was 'yes', it's /s/.
If it's no, it's /k/.
Then I kept going a bit.
I tried partitioning here.
I found that, if I asked 'Is the next letter 'i' ?', that gave this split into /s/ and /k/ and I stopped there.
I'm going to stop growing this tree now because I'm running out of space to draw it.
But in reality we need a better reason to stop!
We need a stopping criterion.
That criterion could be that we can't reduce the entropy by very much, or that there are too few data points left.
Remember that every time we split, we partition the data into smaller and smaller sets and eventually we'll run out of data.
Or we could simply stop when we've reached some certain depth of the tree.
We've reached the end of that sequence on Decision Trees.
Let's repeat this very important distinction between the model and the algorithm.
That's why the material is split across two topics.
In the topic 'Decision Tree', we introduced the model.
In this topic, 'Learning Decision Trees', we introduced the algorithm that is used to learn that model from data.
That's the most important message in this video in fact: this distinction in machine learning between model and algorithm.
It's something people confuse very easily.
So we've now got a general-purpose piece of machine learning - the Decision Tree - which can do classification or regression.
It asks questions about predictors.
In all of my examples, the predictors were categorical things like letters, but they don't have to be.
They could be continuous values that we could ask questions about: 'Are they above or below a certain value?', for example.
This is a very general-purpose piece of machine learning.
It can take predictors of any type and it can predict a predictee that's either categorical or continuous.
We'll find that that could be applied in lots of different places in speech synthesis, from predicting pronunciation to prosody.