In a way, this is the foundation on which almost everything else is built. But don’t be intimidated by maths: it’s just a tool, a language for describing things precisely and unambiguously. If you haven’t studied maths formally since school, then now’s the time to brush off the cobwebs!
Credit: this page was updated by Catherine Lai
There are two levels to this part of the course, depending what stage you are at:
- Preparing your application to a Masters programme: Prepare to apply, and optionally the first few milestones for each section of Prepare to study if you want to put together a really strong application.
- Applied and holding an offer: Prepare to study.
Prepare to apply
For many people, it’s actually just the notation that is the biggest barrier. So, your first step is to conquer mathematical language. Mathcentre has lots of other good material too.
Prepare to study
The key topics that you need to learn are
- Probability and statistics
- Algebra
- Calculus
In general, you can use Jurafsky & Martin as a guide to the kind of maths you’ll encounter in introductory courses.
Our experience is that many people don’t realise that maths is useful (and even fun!) until well out of high school. Even if you dropped it as subject in high school, you can definitely still pick it up later! As an introduction, we like the practice based approach of Khan academy (see below), but if you’re looking for an introductory textbook, Foundations Maths by Croft and Davidson covers the basics and is written specifically for students who have not had specialist maths classes in high school (e.g. A-levels in the UK). It’s available online via the University of Edinburgh library, but you can also find very cheap secondhand copies online.
Make a plan
You need to set yourself some goals and a timeline. We’re suggesting a timeline over the summer before commencing study, but you can of course move everything earlier and spread it over a longer period if you are able to. We’re also assuming you already did everything above: if not, include that in your plan.
June
Have a look at practice problems sets listed below and make a plan of what other units you’ll need to do. For example: do you know what a function is? exponentials and logarithms? what the big Sigma sign means?
Construct a personal study plan. Use the basic milestones below as your guide.
July
Execute your personal study plan.
August
After completing all the basic milestones, go back and complete the extensions. But, if you need more time on the basic milestones, then spend August on those. It’s better to build a really solid foundation of the basics than have a shaky understanding of more advanced material.
Probability and statistics
Probabilistic and statistical methods are pervasive in speech and language processing. Several Semester 1 courses will provide you with some background but the more familiar you are with these topics now, the better. Even though most students will take a course on univariate statistics, most classes will assume that you at least know basic descriptive statistics (e.g. means, variance, z-scores, normal distribution) right from the beginning. Similarly, speech and language courses will assume that you know basic counting techniques (e.g. how many ways can you select this number of objects from this specific set?). These techniques are foundational to the concept of sampling, which you will come across frequently.
Concepts like conditional probability, independence, and Bayes’ rule will also come up time and time again. So, while you might not need a full understanding of this at the very beginning of semester, they will come up relatively quickly and having done some work on these topics will be beneficial.
For more background: Khan Academy Statistics and Probability
Basic milestones
- Practice problems in Summarizing Quantitative Data
- Practice problems in Probability up to and including Experimental Probability
- Practice the permutations and combinations problems in Counting, Permutations and Combinations
- Read through Sharon Goldwater’s primers on Sets and counting and Probability
Extensions
- Complete all practice problems in Probability up to and including “Conditional probability and independence”
- Complete all practice problems in Counting, Permutations and Combinations
- Complete all exercises in Sharon Goldwater’s Probability primer
Algebra
In order to understand most machine learning methods, you will need to know a reasonable amount of algebra. This is especially true for neural networks: even the fanciest architectures can usually be boiled down to a relatively small set of algebraic operations applied in different ways.
For SLP, we mainly need concepts from linear algebra, specifically vectors and matrices. This builds on a lot of foundational concepts that you might need to brush up on. Ideally, we want students to come in at a level where they understand what an eigenvector is (and more importantly what it represents). If you can’t reach that level just now, don’t worry. You can still get by. Certainly, don’t get too worried about calculating determinants of matrices by hand. However, you will at least need to have an intuition of what vectors and matrices represent (in the 3blue1brown videos below) and how to do basic operations on them. Once you have that, aim to understand the concept of alternative co-ordinate systems, change of basis, and eigenvectors. Really understanding the latter means you are now thinking like a mathematician!
For more background: Khan Academy Algebra
Basic milestones
- Watch 3blue1brown series on Linear Algebra
- Practice problems in Vectors
- Practice problems in the Matrices up to and including “Matrix Multiplication” (and ideally up to “Introduction to Matrix Inverses”)
- Read through Sharon Goldwater’s primer on Vectors and complete the practice problems
Extension
- Linear Algebra, all the way to ‘Eigen-everything’
Calculus
Calculus basically comes in two flavours: derivatives (“slopes”) and integrals (“areas”). While they are fundamental components to many speech and language processing methods, you won’t need to actually use the tools here as often as those of probability, statistics and linear algebra. Rather, it’s more a matter of being able to recognize and understand the intuition behind basic differentiation and integration rules so that other important concepts make sense.
For differentiation, the eventual goal is to be able to understand backpropagation in machine learning. You will mostly see integrals in probability, e.g. understanding marginalization or cumulative distributions. In SLP, we deal with both continuous and discrete variables, so it’s important to be able to make the connection between sums over discrete distributions and integrals over cumulative distributions. Again, knowing the rules from memory is less important than understanding what the concepts mean, but going through calculus problems should help identify other topics where you need some revision: e.g., logarithms or trigonometric functions.
In reality, SLP methods almost always use multivariate frameworks. So, you should also aim for a conceptual understanding of what a partial derivative is and, similarly, what it means to integrate over multiple variables.
For more background: Khan Academy Calculus 1
Basic milestones
- Watch 3blue1brown video series on calculus
- Practice problems in Derivatives: chain rule and other advanced topics up to and including “More chain rule practice” including being able to identify different differentiation rules: e.g., constant, sum, difference, power, production rules, and how to differentiate cos(x), sin(x), 𝑒ˣ, and ln(x)
- Go through material on partial derivates (multivariate calculus)
- Practice problems in Integrals, but only “Indefinite integrals of common functions”
- Go through material on double integrals (multivariate calculus)
Extensions
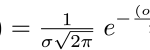

 This is the new version. Still under construction.
This is the new version. Still under construction.